Two groves
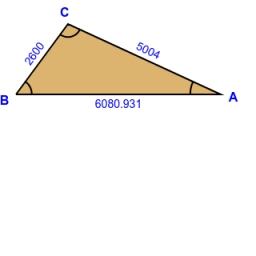
Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- expression of a variable from the formula
- planimetrics
- right triangle
- triangle
- The Law of Cosines
- goniometry and trigonometry
- cosine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Draw triangle
Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm. - Angles
In the triangle ABC, the ratio of angles is α:β = 4:5. The angle γ is 36°. How big are the angles α and β? - Binibini
Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths) - Main/central vertex
ABC is an isosceles triangle with base BC and central vertex A. The angle at vertex A is 18°. What will be the size of the angle at vertex B?
- A cheetah
A cheetah was separated from his brothers on a hunting mission. The brothers were at the watering hole 120 km away. The lost cheetah knew that he had to make it back before sundown, which was 1.5 hours away. His brothers had planned to leave the wateri - Bisectors
As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6. Find the perimeter of triangle △ BDE. - Bisector 2
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
