Dve horárne
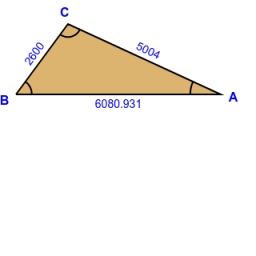
Dve horárne A, B sú oddelené lesom, obe sú viditeľné z horárne C, ktorá je s oboma spojená priamymi cestami. Akú bude mať dĺžku projektovaná cesta z A do B, ak je AC = 5004 m, BC = 2600 m a uhol ABC = 53° 45 '?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- kvadratická rovnica
- vyjadrenie neznámej zo vzorca
- planimetria
- pravouhlý trojuholník
- trojuholník
- kosínusová veta
- goniometria a trigonometria
- kosínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Oblúkom prepojiť
Železnica má prepojiť kruhovým oblúkom miesta A, B a C, ktorých vzdialenosti sú | AB | = 30 km, | AC | = 95 km, | BC | = 70 km. Akú dĺžku bude mať trať z A do C? - Hlavný vrchol
ABC je rovnoramenný trojuholník so základňou BC a hlavným vrcholom A. Uhol pri vrchole A má veľkosť 18°. Akú veľkosť bude mať uhol pri vrchole B? - Trojuholníku 47071
V trojuholníku ABC, pravouhlý uhol je na vrchole B. Strany /AB/=7cm, /BC/=5cm, /AC/=8,6cm. Nájdite na dve desatinné miesta. A. sínus uhla C B. Kosínus C C. Tangenta C. - V pravouhlom 11
V pravouhlom trojuholníku ABC vypočítajte veľkosť vnútorných uhlov, ak/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm.
- Ťažisko a obsah
V trojuholníku ABC sú dané dĺžky jeho ťažníc tc=9, ta=6. Označme T priesečník ťažníc, S stred strany BC. Veľkosť uhla CTS je 60°. Vypočítajte dĺžku strany BC s presnosťou na 2 desatinné miesta - Maturitný - RR - základňa
V rovnoramennom trojuholníku ABC so základňou AB platí ∠BAC = 20°, AB = 4. Os vnútorného uhla pri vrchole B pretína stranu AC v bode P. Vypočítajte dĺžku úsečky AP. Výsledok uveďte s presnosťou na dve desatinné miesta. - V trojuholníku
V trojuholníku ABC je [AB]=20cm, [BC]=10cm, A=30°. Zostroj trojuholník A'B'C' podobný s trojuholníkom ABC, ak koeficient podobnosti je 0,5
