Overhangs 83158
The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rectangular
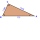Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Right-angled 81150
In the right-angled triangle ABC (the right angle at vertex C), the angle ratio is α : β = 5 : 3. Calculate the sizes of these angles and convert them to degrees and minutes (e.g., 45°20') - Angles
The outer angle of the triangle ABC at vertex A is 147°12'. The outer angle at vertex B is 113°42'. What size is the internal angle at vertex C? - What is 19
What is the length of the hypotenuse c of a right triangle ABC if the angle α at vertex A is 30° and the hypotenuse a = 3cm? - Three vertices
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Right-angled triangle
The right-angled triangle XYZ is similar to the triangle ABC, which has a right angle at the vertex X. The following applies: side a = 9 cm, x=4 cm, x = v-4 (v = height of triangle ABC). Calculate the unknown side lengths of both triangles. - Maturitný - RR - base
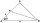In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places.
