Right triangle practice problems - page 6 of 86
Number of problems found: 1720
- Determine 13541
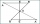The alpha angle is twice the beta angle, and the gamma angle is three times the beta angle. Determine the sizes of all interior angles of the alpha, beta, and gamma triangle ABC. - Right-angled 3511
In a right-angled triangle at vertex C, the alpha angle is 24 degrees smaller than the beta angle to determine the size of the triangle angles. - Base and legs
A right triangle has a base/legs/length of 12 cm, and the angle with the hypotenuse is 13 degrees. What is the length of the second hypotenuse? - In the 18
In the right triangle ABC, The hypotenuse AB = 15 cm, and B = 25 degrees. How long is BC to the nearest centimeter? - The staircase
The staircase has a total height of 3.6 m and forms an angle of 26° with the horizontal. Calculate the length of the whole staircase. - RT triangle and height
Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm. - One side
One side is 36 long with a 15° incline. What is the height at the end of that side? - Spruce height
How tall was the spruce that was cut at an altitude of 8m above the ground, and the top landed at a distance of 15m from the heel of the tree? - Is right triangle or not
If the right triangle is ABC, it has sides a=13, b=11.5, and c=22.5. Find area. - 30-60-90
The longer leg of a 30°-60°-90° triangle measures 14. What is the length of the shorter leg? - Euclid1
The right triangle ABC has hypotenuse c = 20 cm. How large sections cut height hc=9 cm on the hypotenuse c? - Perpendicular 24671
The right triangle has an area of 2304 cm2, and one perpendicular is 8 cm long. Express and calculate the second perpendicular. - Calculate 4424
Calculate the area of the triangle ABC if a = 10 cm, c = 8 cm, ta = 6 cm. - Median in right triangle In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
- The cable car
The cable car is 3,5 kilometers long and climbs at a 30 degrees angle. What is the altitude difference between the Upper and Lower stations? - Isosceles triangle
Calculate the area and perimeter of an isosceles triangle ABC with base AB if a = 6 cm, c = 7 cm. - Triangle ABC
Triangle ABC has side lengths m-1, m-2, and m-3. What has to be m to be a triangle a) rectangular b) acute-angled? - Bevel
I have a bevel in the ratio 1:6. What is the angle, and how do I calculate it? - Right triangle
A right triangle ABC is given, and c is a hypotenuse. Find the length of the sides a, b, the angle beta if c = 5 and angle alfa = A = 35 degrees. - How big is 4
How big is the angle when one side is 20m and the other is 1.5m in a right triangle?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
