Kalkulačka převrácený zlomek
Tato kalkulačka najde převrácenou hodnotu zlomku. Chcete-li najít převrácenou hodnotu zlomku, vyměňte čitatele a jmenovatele. Jednoduše řečeno, převrácená hodnota zlomku a/b je b/a. Výsledný zlomek zjednodušíme.
1 : 3/4 = 4/3 = 1 1/3 ≅ 1,3333333
Jak jsme vyřešili zlomky krok za krokem?
- Dělení: 1 : 3/4 = 1/1 · 4/3 = 1 · 4/1 · 3 = 4/3
První operand je celé číslo. Ekvivalentní je se zlomkem 1/1. Dělení dvou zlomků je stejné jako vynásobení prvního zlomku reciprokou hodnotou druhého zlomku. Prvním dílčím krokem je nalezení reciproké hodnoty (výměna čitatele a jmenovatele, převrácená hodnota 3/4 je 4/3) druhého zlomku. Dále vynásobte dva čitatele. Pak vynásobte dva jmenovatele. Dělení zlomků je vlastně násobení převráceným zlomkem. V dalším mezikroku výslední zlomek není možné dále zjednodušit krácením.
Pravidla výrazů se zlomky:
Znak / je zlomková čára, případně znak dělení - napr. 5/100 nebo 1/2 / 3.Smíšené číslo se skládá z celé části a zlomkové části. Zapisujeme jako celé číslo mezera zlomek. Smíšené číslo (smíšený zlomek) se zapíše např. 1 2/3 (jedna a dvě třetiny).
Desetinná čísla se píší s desetinnou tečkou . nebo čárkou , a automaticky se převedou na zlomky - napr. 1,45.
Dvojtečka : znamená dělení, například na dělení smíšených čísel: 1 2/3 : 4 3/8.
Hvězdička * znamená násobení.
Plus + je sčítání, mínus - je odčítání, () {} [] jsou závorky.
Znak umocnění je ^ - použití například: 1/4^3
Pořadí operací
Přemýšleli jste někdy nad tím, proč kalkulačky nefungují jen zleva doprava? Tato kalkulačka dodržuje matematické pořadí operací – soubor pravidel, která zajišťují, že každý vypočítá výraz stejným způsobem.
Pravidla pořadí operací
1. Závorky - nejprve vyhodnotíme co je v závorkách.
2. Mocniny nebo exponenty
3. Násobení a dělení,
4. Sčítání a odčítání
Základní pravidla
Pravidlo 1: Násobení a dělení vždy provádíme před sčítáním a odečítáním. Představte si je jako VIP, které přeskočí na začátek řady!
Pravidlo 2: Když mají operace stejnou prioritu (jako například × a ÷ nebo + a −), pracujte zleva doprava - stejně jako při čtení knihy.
Pravidlo 3: Závorky mění přirozené pořadí vyhodnocení operací
Zlomky v slovních úlohách:
- Nejjednodušší tvar
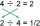Vydělte následující zlomky a zredukujte je na nejjednodušší tvar, pokud je to možné: 1. 2 3/4 ÷ 3 1/12 2. 3 2/3 ÷ 4 1/2 3. 5 3/7 ÷ 2 3/9 4. 6 2/3 ÷ 1 1/5 - 2 krabice pizzy
Na stole zůstaly dvě krabice pizzy stejné velikosti. V jedné krabici je 1/2 pizzy a ve druhé 3/4 pizzy. Potom matka rozdělí všechny pizzy na 1/8. Kolik kousků pizzy zbylo? - Čtvrtina
Čtvrtina z čísla 72 je: - Částka z euro
Jaká část z částky 24 € je 12 €, 4 €, 8 €, 1 €, 18 €, 20 €? - Dělení a násobení zlomků 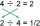Student ví, že ¾ x 4 je totéž jako 4 x ¾ Student předpokládá, že 4 ÷ ¾ je totéž jako ¾ ÷ 4 Má student pravdu?
- Hledání zlomku Můj zlomek není smíšené číslo. Můj zlomek je ekvivalentní 1/2. Když je můj zlomek dělen 1/3, odpověď je 1 1/2. Čtenář zlomku je 4. Jaký je můj zlomek?
- Pizza 3
Pizzerie si účtuje 2 dolary za kus, který je jednou osminou pizzy, a 3 dolary za kus, který je jednou čtvrtinou pizzy. Jednoho dne pizzerie upeče šest pizz. O kolik více peněz vydělají, když všechny pizzy nakrájejí na osminky, jako kdyby je nakrájely na č
slovní úlohy - více »
Poslední změna: 10.3.2026
