Quadratic equation calculator

Quadratic equation has the basic form:

a x^{2} + b x + c = 0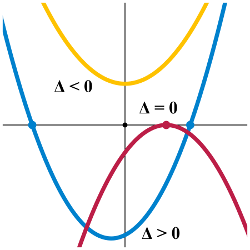

Enter the quadratic equation's coefficients a, b, and c of its basic standardized form. A solution of quadratic equations is usually two different real or complex roots or one double root — the calculation using the discriminant.

Calculation:

140 = 3 * s q r t (3) * a^{2} + 30 a - 5.1961524227066 a^{2} - 30 a + 140 = 0 5.1961524227066 a^{2} + 30 a - 140 = 0 p = 5.196152; q = 30; r = - 140 D = q^{2} - 4 p r = 3 0^{2} - 4 \cdot 5.196152 \cdot (- 140) = 3809.8453567157 D > 0 a_{1, 2} = \frac{- q \pm D}{2 p} = \frac{- 3 0 \pm 3 8 0 9 . 8 5}{1 0 . 3 9 2 3 0 5} a_{1, 2} = - 2.886751 \pm 5.939389 a_{1} = 3.052638008 a_{2} = - 8.8261407 Factored form of the equation: 5.1961524227066 (a - 3.052638008) (a + 8.8261407) = 0

Solution in text:

-5.1961524227066a²-30a+140=0 ... quadratic equation

Discriminant:
D = b² - 4ac = 3809.8453567157
D > 0 ... The equation has two distinct real roots

a₁ = 3.052638
a₂ = -8.8261407

P = {3.052638; -8.8261407}