Quadratic equation calculator
Quadratic equation has the basic form: ax2+bx+c=0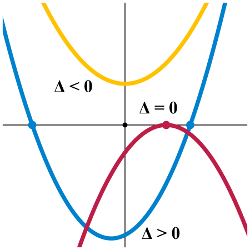
Calculation:
Solution in text:
-2a2+84a-864=0 ... quadratic equationDiscriminant:
D = b2 - 4ac = 144
D > 0 ... The equation has two distinct real roots
a1 = 24
a2 = 18
P = {24; 18}
