Quadratic equation calculator

Quadratic equation has the basic form:

a x^{2} + b x + c = 0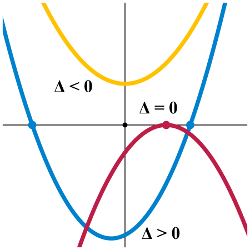

Enter the coefficients a, b, c of quadratic equation in its basic standardized form. A solution of quadratic equations is usually two different real or complex roots or one double root — the calculation using the discriminant.

Calculation:

5 * n (n - 1) = (n + 3) * (n + 2) 4 n^{2} - 10 n - 6 = 0 a = 4; b = - 10; c = - 6 D = b^{2} - 4 a c = 1 0^{2} - 4 \cdot 4 \cdot (- 6) = 196 D > 0 n_{1, 2} = \frac{- b \pm \sqrt{D}}{2 a} = \frac{10 \pm \sqrt{196}}{8} n_{1, 2} = \frac{10 \pm 14}{8} n_{1, 2} = 1.25 \pm 1.75 n_{1} = 3 n_{2} = - 0.5 Factored form of the equation: 4 (n - 3) (n + 0.5) = 0

Solution in text:

4n²-10n-6=0 ... quadratic equation

Discriminant:
D = b² - 4ac = 196
D>0 ... The equation has two distinct real roots

n₁ = 3
n₂ = -0.5

P = {3; -0.5}