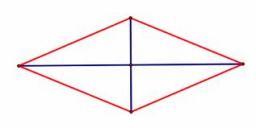
Diagonal
Can a diagonal of a rhombus be equal in length to its side?
Result
Result
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Diagonal
Can it be a diamond diagonal twice longer than its side? - Rhombus and inscribed circle
It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals. - Rhombus
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - The diamond
The diamond has an area S = 120 cm2, and the ratio of the length of its diagonals is e: f = 5:12. Find the lengths of the side and the height of this diamond. - Diagonals in diamons/rhombus
Rhombus ABCD has a side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal. - Diamond
Find the side of the diamond if its area is S = 194 cm² and one diagonal u2 = 44 cm. - Parallelogram - diagonals
Suppose a parallelogram ABCD, the length of one of its diagonals is equal to that of one of its sides. What are the interior angles of this parallelogram?
