Math practice for 13 year olds - page 67 of 422
Number of problems found: 8426
- Suspicion 82035
 At the time of the theft, there were 96 people in the hotel; 61 were beyond suspicion. Of the 47 employees at the hotel, 23 are beyond suspicion. How many guests are not beyond suspicion?
At the time of the theft, there were 96 people in the hotel; 61 were beyond suspicion. Of the 47 employees at the hotel, 23 are beyond suspicion. How many guests are not beyond suspicion? - Together sewing
 Eva sews a costume in 6 hours, Ivana in 8 hours, and Monika in 4 hours. How long will it take them to make the costume if they work together?
Eva sews a costume in 6 hours, Ivana in 8 hours, and Monika in 4 hours. How long will it take them to make the costume if they work together? - Repetition: 82003
 Calculate how many different monograms (short name and surname) I can make from the letters A, E, M, Z, and K. a) with repetition: b) without repetition:
Calculate how many different monograms (short name and surname) I can make from the letters A, E, M, Z, and K. a) with repetition: b) without repetition: - Nationalities 81998
 In the popular Italian resort of Caorle, there are only 4 nationalities. The resort has 3/20 Germans, 2/5 Czechs, 1/4 Austrians, and 500 Brits. How many tourists are there in total at the resort?
In the popular Italian resort of Caorle, there are only 4 nationalities. The resort has 3/20 Germans, 2/5 Czechs, 1/4 Austrians, and 500 Brits. How many tourists are there in total at the resort? - Afforestation workers
 During afforestation, two workers planted 80 seedlings in 2 hours. At the same output, how many seedlings did 6 workers plant in 5 hours?
During afforestation, two workers planted 80 seedlings in 2 hours. At the same output, how many seedlings did 6 workers plant in 5 hours? - Position of digits
 Find a number with six digits. If you put the last digit before the first, you get a new number that is five times larger. The digits between must not change their position.
Find a number with six digits. If you put the last digit before the first, you get a new number that is five times larger. The digits between must not change their position. - Volunteers 81981
 Volunteers planted saplings in the forest nursery; spruces made up 55% of all saplings; one-third were edible, and the rest were young pines. How many saplings did they plant if the number of saplings was greater than 1060 and less than 1090?
Volunteers planted saplings in the forest nursery; spruces made up 55% of all saplings; one-third were edible, and the rest were young pines. How many saplings did they plant if the number of saplings was greater than 1060 and less than 1090? - Together 81979
 Three friends split the reward in the ratio of 3:5:7. One of them received exactly €49. How many euros did they get together?
Three friends split the reward in the ratio of 3:5:7. One of them received exactly €49. How many euros did they get together? - Divided 81973
 A log 88 cm long is divided into 3 parts in the ratio 3: 2: 5. How big is each part?
A log 88 cm long is divided into 3 parts in the ratio 3: 2: 5. How big is each part? - Passenger train
 At 9:15 AM, a passenger train passes the station at a speed of 75 km/h. At 10 o'clock, an express train passes through the same station in the same direction at a speed of 120 km/h. Both trains arrive at the same destination station at the same time. a) a
At 9:15 AM, a passenger train passes the station at a speed of 75 km/h. At 10 o'clock, an express train passes through the same station in the same direction at a speed of 120 km/h. Both trains arrive at the same destination station at the same time. a) a - Probability 81964
 Calculate the probability of the event that you sit in seats 1 to 30 in the cinema at: a) seat marked with a prime number b) seat marked with an even number c) a seat marked with a number divisible by 3 or 4
Calculate the probability of the event that you sit in seats 1 to 30 in the cinema at: a) seat marked with a prime number b) seat marked with an even number c) a seat marked with a number divisible by 3 or 4 - Staircase 81963
 How long is the staircase railing with 17 steps if the step is 32 cm deep and 14.5 cm high? The last step does not count.
How long is the staircase railing with 17 steps if the step is 32 cm deep and 14.5 cm high? The last step does not count. - Dimensions 81957
 How many bricks are needed to build a wall that is 12 m long, 1.6 m high, and 47 cm wide if the dimensions of the brick are 30 x 15 x 7.5 cm and 5% of the wall volume is mortar?
How many bricks are needed to build a wall that is 12 m long, 1.6 m high, and 47 cm wide if the dimensions of the brick are 30 x 15 x 7.5 cm and 5% of the wall volume is mortar? - Propagation 81955
 A plane flying at 612 km/h speed sent a sound signal. In front of the aircraft (in the direction of flight), there is a fixed object at a distance of 3 km, from which the sound is reflected back to the plane. How long will it take the pilot to hear the ec
A plane flying at 612 km/h speed sent a sound signal. In front of the aircraft (in the direction of flight), there is a fixed object at a distance of 3 km, from which the sound is reflected back to the plane. How long will it take the pilot to hear the ec - We randomly
 We randomly select a three-digit number. What is the probability that the number 8 occurs at most once in its notation?
We randomly select a three-digit number. What is the probability that the number 8 occurs at most once in its notation? - Competition 81952
 All three team members took turns fulfilling the competition task without delay. The first member used up 30% of the total competition time. The second needed 10 minutes more than the first, and only 10 minutes remained for the third. What % of the total
All three team members took turns fulfilling the competition task without delay. The first member used up 30% of the total competition time. The second needed 10 minutes more than the first, and only 10 minutes remained for the third. What % of the total - Calculate 81950
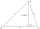 The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle.
The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle. - Inscribed cube
 A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area.
A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area. - Small density cube
 Calculate the mass of a cube with an edge of 15 cm made of oak wood with a density of ρ = 800 kg/m³.
Calculate the mass of a cube with an edge of 15 cm made of oak wood with a density of ρ = 800 kg/m³. - Increased 81943
 The mobile was increased by a quarter of the original price and then again by a quarter of the new price. How much did the mobile cost if its final price was 125 euros?
The mobile was increased by a quarter of the original price and then again by a quarter of the new price. How much did the mobile cost if its final price was 125 euros?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
