Grade - math word problems - page 203 of 949
Number of problems found: 18978
- Supermarket 79504
 The supermarket reduced the original price of the skis by 20% in January. At the beginning of February, they reduced the new price by another 29%. By what percentage were the skis' costs lower than the original price in February?
The supermarket reduced the original price of the skis by 20% in January. At the beginning of February, they reduced the new price by another 29%. By what percentage were the skis' costs lower than the original price in February? - A Petri
 A Petri dish contains 35 cells. Every day, each cell in the Petri dish divides into 2 cells in a process called mitosis. How many cells are there after 14 days?
A Petri dish contains 35 cells. Every day, each cell in the Petri dish divides into 2 cells in a process called mitosis. How many cells are there after 14 days? - A test 3
 A test of five light bulbs showed that they burned for the following lengths of time (in days): 17 2/3, 19 1/4, 20 1/2, 21, and 18 3/4. For how many days, on average, did the light bulbs burn?
A test of five light bulbs showed that they burned for the following lengths of time (in days): 17 2/3, 19 1/4, 20 1/2, 21, and 18 3/4. For how many days, on average, did the light bulbs burn? - Expressed 79474
 The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube.
The length of the cube's edge in cm is expressed as a natural number. Its volume is greater than 100 and less than 200. Calculate the surface area of the cube. - Divisible 79464
 The teacher wrote a number less than 50,000 on the board. The first student said: This number is divisible by 2 The second student said: This number is divisible by 3 And so on, down to the last one who claimed it was divisible by 13. Two in a row lied. W
The teacher wrote a number less than 50,000 on the board. The first student said: This number is divisible by 2 The second student said: This number is divisible by 3 And so on, down to the last one who claimed it was divisible by 13. Two in a row lied. W - Playground 79454
 In Kocourkov, they decided to build a children's playground and volleyball courts. The volleyball court will have dimensions of 18m x 19m. The playground will have a square face. The area of both fields will be the same. What will be the dimensions of t
In Kocourkov, they decided to build a children's playground and volleyball courts. The volleyball court will have dimensions of 18m x 19m. The playground will have a square face. The area of both fields will be the same. What will be the dimensions of t - Paper rolls
 The cost, c, of paper towels, based on the number of rolls, r, is given by this equation: c=1.29r What is the unit rate of the cost of the paper towels in dollars per roll?
The cost, c, of paper towels, based on the number of rolls, r, is given by this equation: c=1.29r What is the unit rate of the cost of the paper towels in dollars per roll? - Leftovers from boards
 The carpenter has three boards 360 cm, 27 dm and 450 cm long, and he wants to cut them into boards of the same length so that there are no leftovers. What will the board be to make it as long as possible?
The carpenter has three boards 360 cm, 27 dm and 450 cm long, and he wants to cut them into boards of the same length so that there are no leftovers. What will the board be to make it as long as possible? - Proportion 79414
 There are 45 seats on the bus. Six passengers are standing, and the remaining 18 are seated. What fraction of passengers are standing? What proportion of passengers are seated? How many seats are unoccupied? How many people would have to be on the bus to
There are 45 seats on the bus. Six passengers are standing, and the remaining 18 are seated. What fraction of passengers are standing? What proportion of passengers are seated? How many seats are unoccupied? How many people would have to be on the bus to - Temperature 79404
 The aluminum coil line has a resistance of 4.6 Ohm at an elevated temperature of 64°C. At what base temperature will the resistance be 2 ohms?
The aluminum coil line has a resistance of 4.6 Ohm at an elevated temperature of 64°C. At what base temperature will the resistance be 2 ohms? - Diala
 Diala bought some books in 2012, and then during 2013, she bought 3 times as many books as she bought in 2012. Diala bought 48 books during these two years. Make a diagram to represent the given. How many books did Diala buy each year?
Diala bought some books in 2012, and then during 2013, she bought 3 times as many books as she bought in 2012. Diala bought 48 books during these two years. Make a diagram to represent the given. How many books did Diala buy each year? - Three-eighths 79384
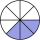 How much is two-sevenths of 420 less than three-eighths of 960?
How much is two-sevenths of 420 less than three-eighths of 960? - Determine 79374
 Determine how many pieces of squares the chocolate would have if, after dividing it into the smallest pieces of the square, we would divide it without remainder between five and three people equally to each person.
Determine how many pieces of squares the chocolate would have if, after dividing it into the smallest pieces of the square, we would divide it without remainder between five and three people equally to each person. - General triangle
 Given a general triangle ABC. Its perimeter is 30 cm, with side a=2 cm longer than side b and 5 cm shorter than side c. Determine the area of the triangle.
Given a general triangle ABC. Its perimeter is 30 cm, with side a=2 cm longer than side b and 5 cm shorter than side c. Determine the area of the triangle. - Acceleration 79354
 A safe jump is considered to be one in which a person hits the ground at a maximum speed of 8m/s. Determine the maximum height from which jumping and landing on the moon is safe. The acceleration on the earth is g= 10 m/s², and the acceleration on the moo
A safe jump is considered to be one in which a person hits the ground at a maximum speed of 8m/s. Determine the maximum height from which jumping and landing on the moon is safe. The acceleration on the earth is g= 10 m/s², and the acceleration on the moo - Yesterday 79344
 Petr played Minecraft for 2 hours yesterday. Pavel played 10% longer. How many minutes did Pavel play?
Petr played Minecraft for 2 hours yesterday. Pavel played 10% longer. How many minutes did Pavel play? - Blackboard 79334
 The biology teacher, Carrot, randomly called the students to the blackboard. There were 25 pupils in the class, and Mr. Carrot called Ludek, Silva, and Mathias. What percentage of the total number of students was called today?
The biology teacher, Carrot, randomly called the students to the blackboard. There were 25 pupils in the class, and Mr. Carrot called Ludek, Silva, and Mathias. What percentage of the total number of students was called today? - The angles 3
 The angles in a triangle are in the ratio of 3:4:5. Work out the size of each angle.
The angles in a triangle are in the ratio of 3:4:5. Work out the size of each angle. - Corresponding 79314
 On the circular face of the clock, we connect the points corresponding to the numbers 2, 9, and 11, which creates a triangle. Calculate the sizes of all the interior angles of that triangle.
On the circular face of the clock, we connect the points corresponding to the numbers 2, 9, and 11, which creates a triangle. Calculate the sizes of all the interior angles of that triangle. - Mr. Stratton
 Mr. Stratton has a flower garden. Of the flowers in his garden, 1/3 of them are roses, and 3/5 of the roses are red. What fraction of Mr. Stratton's flowers are red roses?
Mr. Stratton has a flower garden. Of the flowers in his garden, 1/3 of them are roses, and 3/5 of the roses are red. What fraction of Mr. Stratton's flowers are red roses?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
