Examples for secondary school students - page 51 of 231
Number of problems found: 4604
- All multiples
 Set A is a set of all multiples of 2, and set B is a set of all multiples of 3. If the P (A)=0.6 and P (B)=0.3. Find P (AUB).
Set A is a set of all multiples of 2, and set B is a set of all multiples of 3. If the P (A)=0.6 and P (B)=0.3. Find P (AUB). - Possibility 65535
 The bank offers a term account with the possibility of early withdrawal with an interest rate of 1.85 percent pa. Milan put 2,500 euros on it on January 2. If he withdraws the money after eight months, how many euros will he get?
The bank offers a term account with the possibility of early withdrawal with an interest rate of 1.85 percent pa. Milan put 2,500 euros on it on January 2. If he withdraws the money after eight months, how many euros will he get? - Interest 65494
 Martina invested 1,300 euros in the bank, and after a year, the bank credited her with an interest of 26.65 euros. What was this bank's annual interest rate?
Martina invested 1,300 euros in the bank, and after a year, the bank credited her with an interest of 26.65 euros. What was this bank's annual interest rate? - An aircraft 2
 An aircraft jet engine has a thrust of 80 kN. What impulse is produced in 30 seconds?
An aircraft jet engine has a thrust of 80 kN. What impulse is produced in 30 seconds? - Calculate sphere cap
 Calculate the surface of a spherical cap with a height of 6 cm and a radius of 15 cm
Calculate the surface of a spherical cap with a height of 6 cm and a radius of 15 cm - Parallelogram 65334
 In a parallelogram, the sum of the lengths of the sides a+b = 234. The angle subtended by the sides a and b is 60°. The diagonal size against the given angle of 60° is u=162. Calculate the sides of the parallelogram, its perimeter, and its area.
In a parallelogram, the sum of the lengths of the sides a+b = 234. The angle subtended by the sides a and b is 60°. The diagonal size against the given angle of 60° is u=162. Calculate the sides of the parallelogram, its perimeter, and its area. - Third-graders 65204
 Forty-eight high school students took part in the chess tournament. The number of first-graders, sophomores, and third-graders is 3:8:5. Calculate what percentage of sophomores participated in the game.
Forty-eight high school students took part in the chess tournament. The number of first-graders, sophomores, and third-graders is 3:8:5. Calculate what percentage of sophomores participated in the game. - Substituted 65024
 Which number should be substituted for the variable in the equation: 4x² (7-x) = a-3- (x-2), so that the root of the equation is the number 5?
Which number should be substituted for the variable in the equation: 4x² (7-x) = a-3- (x-2), so that the root of the equation is the number 5? - Horizontally 64874
 How many ways can an arranger display five different shampoos horizontally next to each other?
How many ways can an arranger display five different shampoos horizontally next to each other? - Horizontal 64864
 The meter stick is located on the meridian plane and deviated from the horizontal plane to the north by an angle of magnitude 70°. Calculate the length of the shadow cast by a meter stick at true noon if the Sun culminates at an angle of 41°03'.
The meter stick is located on the meridian plane and deviated from the horizontal plane to the north by an angle of magnitude 70°. Calculate the length of the shadow cast by a meter stick at true noon if the Sun culminates at an angle of 41°03'. - Magnitudes 64704
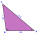 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Sons
 The father has six sons and ten identical, indistinguishable balls. How many ways can he give the balls to his sons if everyone gets at least one?
The father has six sons and ten identical, indistinguishable balls. How many ways can he give the balls to his sons if everyone gets at least one? - Triangle angles
 In the triangle ABC, a: b = 3:2 and α: β = 2:1. Calculate the ratio a: c.
In the triangle ABC, a: b = 3:2 and α: β = 2:1. Calculate the ratio a: c. - Triangle from sticks
 Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks?
Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks? - 14 sticks
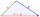 I was cleaning up my attic recently and found a set of at least 14 sticks which a curious Italian sold me some years ago. Trying hard to figure out why I bought it from him, I realized that the set has the incredible property that there are no three stick
I was cleaning up my attic recently and found a set of at least 14 sticks which a curious Italian sold me some years ago. Trying hard to figure out why I bought it from him, I realized that the set has the incredible property that there are no three stick - Two artillery
 Objective C we observe from two artillery observatories, A and B, which are 975 m apart. The size of the BAC angle is 63°, and the size of ABC is 48°. Calculate the distance of points A and C.
Objective C we observe from two artillery observatories, A and B, which are 975 m apart. The size of the BAC angle is 63°, and the size of ABC is 48°. Calculate the distance of points A and C. - Parallelogram 64414
 The parallelogram has side a = 58cm and diagonals u = 89cm and v = 52cm. Calculate the perimeter and area of this parallelogram.
The parallelogram has side a = 58cm and diagonals u = 89cm and v = 52cm. Calculate the perimeter and area of this parallelogram. - Arithmetic 64394
 Karolína does not want to reveal at home what grades she will get on her report card. She said only this: "There will be 8 marks on the report card, their arithmetic mean is 2.125, the median is 2, the mode is 1, and I will not have any 2's. How many four
Karolína does not want to reveal at home what grades she will get on her report card. She said only this: "There will be 8 marks on the report card, their arithmetic mean is 2.125, the median is 2, the mode is 1, and I will not have any 2's. How many four - Observation angle
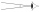 At what angle of view does an object 70 m long appear to the observer, 50 m away from one end and 80 m from the other end?
At what angle of view does an object 70 m long appear to the observer, 50 m away from one end and 80 m from the other end? - Douglas HS
 Douglas High School is holding a fundraiser and plans to use 2/3 of the money collected to build a new library. Of the money directed towards building the new library, 1/5 will purchase computers. What fraction of the money raised will go towards purchasi
Douglas High School is holding a fundraiser and plans to use 2/3 of the money collected to build a new library. Of the money directed towards building the new library, 1/5 will purchase computers. What fraction of the money raised will go towards purchasi
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
