Latest word problems - page 5 of 11

Number of problems found: 218

The rhombus (a,d)
Find the area of a rhombus, one side of which measures 20 cm, and one diagonal 24 cm.
Rectangle - S2
I need help calculating the area and perimeter of a rectangle with a length of 8 cm and a width of 5 cm.
Two masons
Mason A can build a wall in 30 days, while mason B can build it in 40 days. If they build it together and get a payment of USD 7000, what is B's share?
128 USD
128 USD is increased by 20 percentage. Determine the new amount.
A tree 3
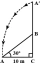A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Doubling - simple interest
A sum becomes its double in 10 years. Find the annual rate of simple interest
Body temperature
Susan temperature is 2.5 degree Celsius above normal. What is her temperature?
The length 20
The length and breadth of a rectangular park are in the ratio 8:5. A path,1.5 m wide, running all around the outside of the park has an area of 594 sq m. Find the dimensions of the park.
A field
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field.
The average 17
The average monthly salary of 20 workers in an office is $4590 . If the manage's salary is added, the average salary becomes $ 4920 per month What's the manager's monthly salary?
The product 18
The product of two consecutive natural numbers which are multiples of 3 is equal to 810. Find the two numbers.
Four numbers 3
What least number must be added to each of the numbers 6,15,20 and 43 to make them proportional?
The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower
Surface = volume
If the volume and the surface area of a sphere are numerically the same then find its radius.
Triangle - same sides
Can the sides of a triangle have lengths of 11, 11, and 14? If so, what kind of triangle is it?
GP - terms
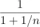Which term of the G.P., 2, 8, 32, ... up to n terms is 131072?
How many 147
How many consecutive natural numbers from 1 to n do you have to add up at least so that their sum exceeds 1000000?
Quarter of some number
A quarter of an unknown number increased by one hundred is fifty. What is the unknown number?
Spherical sector
Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm.
Third angle
What is the third angle of a triangle if the first two angles have sizes 50° and 60°?

Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.