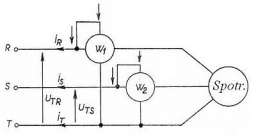
3 phase load
Two wattmeters are connected to measure power in a 3 phase balanced load. Determine the total power and power factor if the two wattmeters read 1000 watts each (1) both positive and (2) the second reading is negative.
Correct answer:
Tips for related online calculators
Do you want to convert time units like minutes to seconds?
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
goniometry and trigonometryUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Two resistors 5
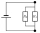Two resistors are connected in parallel. The first resistor has a resistance of 2000 ohms and a current of 4 mA flows through it. The second resistor has a resistance of 1600 ohms. 1/Draw a circuit diagram 2/Determine the voltage of the power source. 3/Wh - Andy and Mike
Mike and Andy are each reading the same book. Mike read 2/4 of the book on Tuesday and 1/3 of the book on Wednesday. Andy read 1/2 of the book on Tuesday and 1/5 of the book on Wednesday. Andy says that altogether he read more of the book on Tuesday and W - Quadratic equation - Viets
In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas. - Variables: 3140
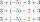Determine the value of the expression 3a + 2b - a² - 4b² for the values of the variables: a) a = - 1, b = 3 b) a = 2, b = -1 c) a = -2, b = -3 d) a = 4, b = 2 e) a = -5, b = 0 - Fransisca Fransisca read a book 391 pages long, reading 17 pages a day. There are two more books in the series. How long will it take Fransisca to read all three books if they have the same page length and she reads at the same speed?
- Open and short circuit tests
A 4 kVA 200/400 V single phase 50 Hz transformer has the following data on O. C. (open circuit) & S. C. (short circuit) test: O. C. Test: 200 V 0.8 A 70 W (Low Voltage side) S. C. Test: 20 V 10 A 80 W (High Voltage side) Find Full Load efficiency and regu - Line
Straight-line passing through points A [-3; 22] and B [33; -2]. Determine the total number of points of the line in which both coordinates are positive integers.
