Wallpaper
3750 cm square of wallpaper is needed to glue a cube-shaped box. Can Dad cut out the whole necessary piece of wallpaper if he has a roll of wallpaper 50 cm wide?
Your answer:
Your answer:
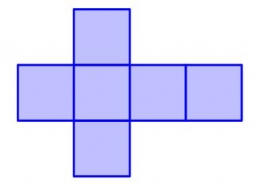
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Castle model
The castle model has a cone-shaped roof. The cone side is 45 cm long, and the base radius is 27 cm. a) What is the roof volume? b) How much dm² of wallpaper is used to glue the roof, i.e., the cone shell? c) What is the roof's weight if it is made of wood - Roll of wallpaper
An art student uses a roll of wallpaper to decorate two gift boxes. The student will use 3 1/3 yards of paper for one box and 5/6 yards of paper for the other box. He must cut the paper into pieces that are 1/6 yard long. How many pieces will the student - Painter 3
Dad wants to paint the wall high 250 cm, wide 230 cm with wallpaper. How many meters must he buy wallpaper if the wallpaper width is 60 cm? - Wallpaper - box network
How much dm² of wallpaper is needed to stick a box (without a lid) in the shape of a cube with an edge of 12 dm? - Box metal
A box is shaped like a cube with an edge of 52 cm. How many m² of sheet metal are needed to make the box with a lid? Add 5% for the folds of the lid and walls. - Box cube paper
The open box has the shape of a cube. We used 80 dm² of paper to glue on it. What is the volume of this box? - Bulletin board
Tripp and Paul are using yellow craft paper to cover a bulletin board. The board is 11 feet wide and 7 feet tall. The craft paper comes in a roll that is 1 yard wide. They can roll it out and cut it to any length, but the paper will always be 1 yard wide.
