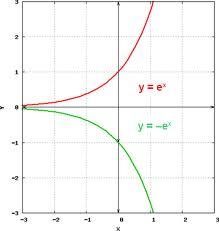
Exponential equation

In the set R, solve the equation:

7^{- 5 + 19 x} = 4^{3 - 20 x}

Final Answer:

Did you find an error or inaccuracy? Feel free to send us. Thank you!

You need to know the following knowledge to solve this word math problem:

algebra

exponential equation

basic operations and concepts

Grade of the word problem

high school

Related math problems and questions:

Following 2896
Solve the following set of equations with three unknowns. 3x + 2y + 3z = 110 5x-y-4z = 0 2x-3y + z = 0
Equation
Solve the equation and check the result: 1.6x - 3/2 + x - 9,8 = x + 0,4/3 - 7 + 1,6/6
Linear system
Solve a set of two equations of two unknowns: 1.5x+1.2y=0.6 0.8x-0.2y=2
Equation 6738
Solve the given equation in the set N: 1 - x + x² - x³ + x⁴ - x⁵ +…. + = 1/3
Equation: 6200
Solve the equation: 2y = 4 (0.5 + 3/2) -1
Equation 25
Solve the following simple equation: 3/4(x+5)=1/2(x+9)
Diofant equation
In the set of integers (Z), solve the equation: 212x +316y =0 Write result with integer parameter t in Z (parameter t = ...-2,-1,0,1,2,3... if equation has infinitely many solutions)