Assembly time
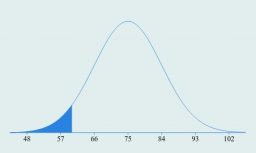
The assembly time for the toy follows a normal distribution with a mean of 75 minutes and a standard deviation of 9 minutes. The company closes at 5 pm every day. If one starts assembling at 4 pm, what is the probability that he will finish before the company closes for the day?
Correct answer:
Showing 1 comment:
Math Teacher
We use an online normal distribution calculator for this:
https://www.hackmath.net/en/calculator/normal-distribution?mean=75&sd=9&above=&area=below&below=60&ll=&ul=&outsideLL=&outsideUL=&draw=Calculate
https://www.hackmath.net/en/calculator/normal-distribution?mean=75&sd=9&above=&area=below&below=60&ll=&ul=&outsideLL=&outsideUL=&draw=Calculate
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
Looking for a standard deviation calculator?
Would you like to compute the count of combinations?
Looking for a statistical calculator?
Looking for a standard deviation calculator?
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
statisticscombinatoricsGrade of the word problem
Related math problems and questions:
- Lifetime - bell curve
Laser lifetime follows a normal distribution with a mean of 7000 hours and a standard deviation of 600 hours. What is the probability that the laser will fail before 6000 hours? What is the probability that the laser will last at least 7500 hours? - Distribution if the IQ
Assume that the IQ in the population follows a normal distribution with a mean of 100 points and a standard deviation of 10 points. With what probability among 15 randomly selected people: a. Is there anyone with an IQ above 130 points? b. Are there at le - Bulb life
Tests show that the lives of light bulbs are normally distributed with a mean of 750 hours and a standard deviation of 75 hours. Find the probability that a randomly selected light bulb will last between 675 and 900 hours. - The average 7
The average lifespan for cricket is 90 days, with a standard deviation of 13 days. If we assume that the lifespan of cricket is normally distributed, a. What is the probability a randomly selected cricket has a lifespan of fewer than 75 days? b. What is t - Suppose 6
Suppose the life span of a revolutionary light bulb is normally distributed with a mean life span of 70 thousand hours and a standard deviation of 3 thousand hours. If a light bulb is chosen at random: a) what is the probability the life span will be with - The usage
The battery usage time installed in a particular smartphone has a Normal distribution with a mean of 25.2 hours and a standard deviation of 7.5 hours. What is the probability of usage time greater than 32? - Probability
A restaurant always takes an inventory at the cash register at the end of the day so that the employees can divide their tips. It has been found that the daily tips follow a normal distribution with a mean of €130 and a standard deviation of 60. What is t
