Rope
How many meters of rope 10 mm thick will fit on the bobbin diameter of 200 mm and a length of 350 mm (the central mandrel has a diameter of 50 mm)?
Final Answer:

Tips for related online calculators
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Winch
 The steel rope has a diameter of 6mm and a length of 20m. We are winding it on a drum width of 60 mm, with a starting diameter of 50 mm. What is the final diameter after winding?
The steel rope has a diameter of 6mm and a length of 20m. We are winding it on a drum width of 60 mm, with a starting diameter of 50 mm. What is the final diameter after winding? - House extension
 Igor is going to build an extension. He has 3 perimeter load-bearing walls, 9.1 m, 6.5 m, and 10 m long. 3 m high. There are two windows: 2 m x 1.5 m. How many blocks measuring 500x250x375 mm should be used to build a wall 375 mm thick? How many pallets a
Igor is going to build an extension. He has 3 perimeter load-bearing walls, 9.1 m, 6.5 m, and 10 m long. 3 m high. There are two windows: 2 m x 1.5 m. How many blocks measuring 500x250x375 mm should be used to build a wall 375 mm thick? How many pallets a - Well
 A rope with a bucket is fixed on the shaft with the wheel. The shaft has a diameter of 45 cm. How many meters will drop bucket when the wheels turn 7 times?
A rope with a bucket is fixed on the shaft with the wheel. The shaft has a diameter of 45 cm. How many meters will drop bucket when the wheels turn 7 times? - Diameter of a drum
 Winding drum length 180mm, initial diameter 60mm. Using a 6mm rope with a length of 50m, what will be the diameter of the wound drum with the rope?
Winding drum length 180mm, initial diameter 60mm. Using a 6mm rope with a length of 50m, what will be the diameter of the wound drum with the rope? - Pipe cross section
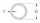 The pipe has an outside diameter of 1100 mm, and the pipe wall is 100 mm thick. Calculate the cross-section of this pipe.
The pipe has an outside diameter of 1100 mm, and the pipe wall is 100 mm thick. Calculate the cross-section of this pipe. - Textbooks
 A math textbook is 1 4/7 inches thick. How many of these books will fit on a 22-inch self?
A math textbook is 1 4/7 inches thick. How many of these books will fit on a 22-inch self? - The coil
 How many ropes (a diameter of 8 mm) fit on the coil (threads are wrapped close together)? The coil has the following dimensions: The inner diameter is 400mm. The outside diameter is 800mm. The length of the coil is 470mm.
How many ropes (a diameter of 8 mm) fit on the coil (threads are wrapped close together)? The coil has the following dimensions: The inner diameter is 400mm. The outside diameter is 800mm. The length of the coil is 470mm.
