Square sides
If the square side increases by 28%, the square circumference increases by 11.2 meters. Find the length of the original square side.
Final Answer:

Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circumference 3170
 Suppose we enlarge the side of the square by half the length, and the circumference of the square increases by 24 cm. Calculate the original side length.
Suppose we enlarge the side of the square by half the length, and the circumference of the square increases by 24 cm. Calculate the original side length. - Square
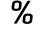 The square's side length decreases by 25%, and its area is now 28 cm22 lower. Find the side of the original square.
The square's side length decreases by 25%, and its area is now 28 cm22 lower. Find the side of the original square. - Table
 Find the table's circumference; the long side is 1.28 meters, and the short side is 86 cm.
Find the table's circumference; the long side is 1.28 meters, and the short side is 86 cm. - Square sides
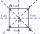 If we enlarge the side of the square by a third, its circumference will be 20 cm larger than the original. What is the side of the square?
If we enlarge the side of the square by a third, its circumference will be 20 cm larger than the original. What is the side of the square? - Circumference of a rhombus
 If you enlarge the side of the diamond by 4 cm, its circumference will be 20 cm. How long was the side of the original diamond?
If you enlarge the side of the diamond by 4 cm, its circumference will be 20 cm. How long was the side of the original diamond? - Circumference 17533
 If we enlarge the side of the square by half, its circumference will be 24 cm larger than the original. What is the side of the square?
If we enlarge the side of the square by half, its circumference will be 24 cm larger than the original. What is the side of the square? - A number 4
 A number is made up of two digits. The sum of the digits is 11. if the digits are interchanged, the original number increases by 9. Find the original number
A number is made up of two digits. The sum of the digits is 11. if the digits are interchanged, the original number increases by 9. Find the original number
