Inverse matrix
Find out the inverse using Gauss elimination or the reduction method.
A=[2/3. 1
-3. 1/3]
A=[2/3. 1
-3. 1/3]
Final Answer:
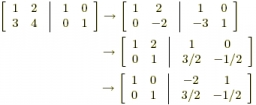
Tips for related online calculators
Do you have a system of equations and are looking for calculator system of linear equations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Elimination method
 Solve the system of linear equations by elimination method: 5/2x + 3/5y= 4/15 1/2x + 2/5y= 2/15
Solve the system of linear equations by elimination method: 5/2x + 3/5y= 4/15 1/2x + 2/5y= 2/15 - Square root by hand
 Estimate √38 to the nearest hundredths, using any of the two methods (divide and average method or square root estimate formula).
Estimate √38 to the nearest hundredths, using any of the two methods (divide and average method or square root estimate formula). - Completing square
 Solve the quadratic equation: m²=4m+20 using completing the square method.
Solve the quadratic equation: m²=4m+20 using completing the square method. - Parallel lines - dist
 Find the distance between the parallel lines 3x – 4y +7 = 0 and 3x – 4y + 5 = 0
Find the distance between the parallel lines 3x – 4y +7 = 0 and 3x – 4y + 5 = 0 - Lie/do not lie
 The rule f(x) = -x-10 gives the function. Find whether point C[5; -15] lies on this function. Solve graphically or numerically and give reasons for your answer.
The rule f(x) = -x-10 gives the function. Find whether point C[5; -15] lies on this function. Solve graphically or numerically and give reasons for your answer. - Three cats
 If three cats eat three mice in three minutes, after which time 70 cats eat 70 mice?
If three cats eat three mice in three minutes, after which time 70 cats eat 70 mice? - Government 4253
 The government had saved a few cents. They added another 60 cents. He missed 90 cents in the school cafeteria. He has 284 cents left in the treasury. How many cents did Vlado save?
The government had saved a few cents. They added another 60 cents. He missed 90 cents in the school cafeteria. He has 284 cents left in the treasury. How many cents did Vlado save?
