Completing square
Solve the quadratic equation: m2=4 m+20 using completing the square method.
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Exponential equation
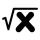Determine m (solve the exponential equation - unknown in the exponent): 0.25 μm = 0.5 - Force Between Charged Balls
Calculate the force between two balls with charges of +3 μC and −4 μC when they are 60 mm apart. Calculate the force in a vacuum (k = 9 × 10⁹ N·m²/C²). - Function
For linear function f(x) = ax + b is f(19)=141; f(20)=168. Calculate m, if f(m) = 2018. - Suppose 5
Suppose z5=2+3i and z6=6+9i are complex numbers and 3 z5 + 7 z6= m+in. What is the value of m and n? - Together m+w
Women are 30%. Men are 360 more. How many are together? - Together m+d
Aunt Jane would paint her apartment in 10 hours and her mother in 15 hours. How much do they paint it together? - Temperature linear fit
At 2:00 a.m., the temperature was -7 °F. At noon the temperature was 18 °F. What expression represents the increase in temperature?
