Math practice for 13 year olds - page 113 of 422
Number of problems found: 8425
- Calculate 66814
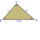 Calculate the area and perimeter of the right triangle ABC if A [5.5; -2.5] B [-3; 5] C [-3; -2.5]
Calculate the area and perimeter of the right triangle ABC if A [5.5; -2.5] B [-3; 5] C [-3; -2.5] - Performance 66764
 Six masons of equal performance were able to plaster the walls of the new garages in 18 shifts. After 4 shifts of joint plastering, 2 got sick. a) In how many more shifts did the masons complete the said plastering? b) In how many shifts was the assigned
Six masons of equal performance were able to plaster the walls of the new garages in 18 shifts. After 4 shifts of joint plastering, 2 got sick. a) In how many more shifts did the masons complete the said plastering? b) In how many shifts was the assigned - Expression 66754
 Find the largest natural number n for which the expression value (37-2n) / 3 equals the natural number.
Find the largest natural number n for which the expression value (37-2n) / 3 equals the natural number. - Percentage - rhombus
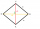 If the rhombus side in the image increases by half, by what percentage will the area of the rhombus increase?
If the rhombus side in the image increases by half, by what percentage will the area of the rhombus increase? - Percentage 66714
 They cut a full circle from a square plate with a side of 200 mm. What percentage is waste?
They cut a full circle from a square plate with a side of 200 mm. What percentage is waste? - Northeast 66694
 Katka and Honza rode out on their scooters at the same time. Katka drove at a speed of 4.5 km/30 min, and Honza drove at a speed of 4 km/20 min. a) how many m did they travel in 2 minutes if they went in the opposite direction? b) how many miles did they
Katka and Honza rode out on their scooters at the same time. Katka drove at a speed of 4.5 km/30 min, and Honza drove at a speed of 4 km/20 min. a) how many m did they travel in 2 minutes if they went in the opposite direction? b) how many miles did they - Percentage - prism and cube
 Prism with square base a=25cm, height h=45cm. cube: b=15cm a) what percentage of the volume of the prism is the volume of the cube? b) what height should the prism have to have the same volume as the cube?
Prism with square base a=25cm, height h=45cm. cube: b=15cm a) what percentage of the volume of the prism is the volume of the cube? b) what height should the prism have to have the same volume as the cube? - Terminated 66674
 The department store originally employed 8 cleaners for reduced working hours of 4 hours a day. When two of them terminated their employment, 6 cleaners agreed to extend their original daily working hours. Specify its length in hours and minutes.
The department store originally employed 8 cleaners for reduced working hours of 4 hours a day. When two of them terminated their employment, 6 cleaners agreed to extend their original daily working hours. Specify its length in hours and minutes. - Probability 66644
 Oskar observes the arrivals and departures of cars in the parking lot. At one point, there were 99 cars in the parking lot: 25 red, 17 white, and the rest were black. What is the percentage probability that a black car was leaving the parking lot at a giv
Oskar observes the arrivals and departures of cars in the parking lot. At one point, there were 99 cars in the parking lot: 25 red, 17 white, and the rest were black. What is the percentage probability that a black car was leaving the parking lot at a giv - Represented 66634
 On a map with a scale of 1:30,000, the plot is represented by a square with a side of 6 cm. What is the area really like? How many times is the actual plot larger than its image on the map?
On a map with a scale of 1:30,000, the plot is represented by a square with a side of 6 cm. What is the area really like? How many times is the actual plot larger than its image on the map? - Quadrilateral 66614
 The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm².
The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm². - Hexagonal wax
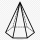 The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax.
The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax. - Percentage - b/g students
 There are 584 students at the school, 421 of them boys. What percentage of students are girls?
There are 584 students at the school, 421 of them boys. What percentage of students are girls? - O'clock 66554
 What is the angle of the hour and minute hands on the clock of the old tower if it is exactly eight o'clock?
What is the angle of the hour and minute hands on the clock of the old tower if it is exactly eight o'clock? - Conditions 66544
 I have a box that contains white, milk, and dark chocolate candies. The ratio of white to milk candies is 3:4. The ratio of white to dark candies is 4:3. The least amount of candies in the box if the conditions of the ratio of candies are met.
I have a box that contains white, milk, and dark chocolate candies. The ratio of white to milk candies is 3:4. The ratio of white to dark candies is 4:3. The least amount of candies in the box if the conditions of the ratio of candies are met. - 15-kilogram 66524
 The lift has a load capacity of 250 kg. How many 15-kilogram boxes can a person weighing 80 kg maximally take?
The lift has a load capacity of 250 kg. How many 15-kilogram boxes can a person weighing 80 kg maximally take? - Prepared 66494
 Benches were prepared around the fire. When seven tourists sit on them, one tourist will sit alone on the last bench. When six of them all sat down, one had to stand. How many tourists were at the campfire if we know there were less than 100, and how many
Benches were prepared around the fire. When seven tourists sit on them, one tourist will sit alone on the last bench. When six of them all sat down, one had to stand. How many tourists were at the campfire if we know there were less than 100, and how many - Coordinates 66474
 Draw a trapezoid in the coordinate system with bases 4cm long, 2cm long, and 3cm high. Please write down the coordinates of its vertices.
Draw a trapezoid in the coordinate system with bases 4cm long, 2cm long, and 3cm high. Please write down the coordinates of its vertices. - Performance 66404
 A person weighing 50 kg can climb 15 stairs. One step is 18 cm high. Determine a person's performance when: a) slowly climbing the stairs if it took him 13 seconds b) going down the stairs slowly if it took him 10 seconds c) quickly climbing the stairs if
A person weighing 50 kg can climb 15 stairs. One step is 18 cm high. Determine a person's performance when: a) slowly climbing the stairs if it took him 13 seconds b) going down the stairs slowly if it took him 10 seconds c) quickly climbing the stairs if - Right-angled 66364
 From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area.
From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
