Angle practice problems - page 31 of 64
Number of problems found: 1262
- The aspect ratio
 The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle.
The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle. - Ladder slope
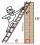 What is the slope of a ladder 6.2 m long and 5.12 m in height?
What is the slope of a ladder 6.2 m long and 5.12 m in height? - Acute angles
 Sizes of acute angles in the right-angled triangle are in the ratio 1:8. What is the size of the larger of them?
Sizes of acute angles in the right-angled triangle are in the ratio 1:8. What is the size of the larger of them? - It is rectangular?
 The size of two of the angles in a triangle is α=110°, β=40°. Is it a right triangle?
The size of two of the angles in a triangle is α=110°, β=40°. Is it a right triangle? - Interior angles - sum
 For the sum s of the interior angles of a polygon, where n is the number of its sides, the relation s=(n−2)⋅180 degrees applies. How many sides does a polygon have if the sum of its interior angles is 900°?
For the sum s of the interior angles of a polygon, where n is the number of its sides, the relation s=(n−2)⋅180 degrees applies. How many sides does a polygon have if the sum of its interior angles is 900°? - Determine 19953
 The distance between the tip of the minute hand and the center of the dial is 12 mm. Determine the distance traveled by the tip in 45 min. (draw a clock face and a minute hand and realize the distance it will cover in 45 min.)
The distance between the tip of the minute hand and the center of the dial is 12 mm. Determine the distance traveled by the tip in 45 min. (draw a clock face and a minute hand and realize the distance it will cover in 45 min.) - Road
 The angle of a straight road is approximately 12 degrees. Determine the percentage of this road.
The angle of a straight road is approximately 12 degrees. Determine the percentage of this road. - Triangle
 Calculate the area of the right triangle ΔABC if one leg is long 12 and its opposite angle is 47°.
Calculate the area of the right triangle ΔABC if one leg is long 12 and its opposite angle is 47°. - Descent of road
 The road sign informs us the gradient is 10.9%. Calculate the angle at which the average decreases.
The road sign informs us the gradient is 10.9%. Calculate the angle at which the average decreases. - Circle 7794
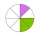 Draw a circle k, r = 4cm, and divide it into two parts in a ratio of 1:5.
Draw a circle k, r = 4cm, and divide it into two parts in a ratio of 1:5. - Coefficient 81704
 In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4.
In the equation of the line p: ax-2y+1=0, determine the coefficient a so that the line p: a) it formed an angle of 120° with the positive direction of the x-axis, b) passed through point A[3,-2], c) was parallel to the x-axis, d) had a direction of k = 4. - Trapezoid v3
 The isosceles trapezoid has an angle at the first base 40 degrees less than the angle at the second base. How large angles has this trapezoid?
The isosceles trapezoid has an angle at the first base 40 degrees less than the angle at the second base. How large angles has this trapezoid? - A man 7
 A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles toward N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.)
A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles toward N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.) - Bisectors
 As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6. Find the perimeter of triangle △ BDE.
As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6. Find the perimeter of triangle △ BDE. - Angles ratio
 The internal angles of a triangle are in ratio 1:4:5. What kind of triangle is it? (solve interior angles and write down and discuss)
The internal angles of a triangle are in ratio 1:4:5. What kind of triangle is it? (solve interior angles and write down and discuss) - Isosceles triangle
 What are the angles of an isosceles triangle ABC if its base is long a=7 m and has an arm b=9 m?
What are the angles of an isosceles triangle ABC if its base is long a=7 m and has an arm b=9 m? - Bisector 2
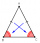 ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - An angle
 An angle x is opposite side AB which is 10, and side AC is 15, which is the hypotenuse side in triangle ABC. Calculate angle x.
An angle x is opposite side AB which is 10, and side AC is 15, which is the hypotenuse side in triangle ABC. Calculate angle x. - The amphitheater
 The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle?
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - Quadrilateral and angles
 In a quadrilateral, angle α is twice as large as angle β. Angle γ is 80% of angle α, and angle δ is 30° greater than angle α. Determine the angles of this quadrilateral.
In a quadrilateral, angle α is twice as large as angle β. Angle γ is 80% of angle α, and angle δ is 30° greater than angle α. Determine the angles of this quadrilateral.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
