Examples of area of plane shapes - page 21 of 131
Number of problems found: 2604
- Circumscribed 7290
 Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm.
Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm. - Calculate 5255
 The area of the square is equal to 2.56 square meters. Calculate its diagonal.
The area of the square is equal to 2.56 square meters. Calculate its diagonal. - Playground 2908
 The fencing of the square playground cost € 462, while the 1m fencing cost € 11. What is its playground area?
The fencing of the square playground cost € 462, while the 1m fencing cost € 11. What is its playground area? - Path 11
 A path 1.5 meters wide is to be built around the perimeter of a square plot of land with a side of 28 meters. By how much will the area of the plot be reduced?
A path 1.5 meters wide is to be built around the perimeter of a square plot of land with a side of 28 meters. By how much will the area of the plot be reduced? - Determine the area
 Determine the area of the trapezoid ABCD, in which the following holds: AB= 6cm, Area of triangle ABC= 15 cm2, area of triangle BCD= 20 cm2, AB||CD.
Determine the area of the trapezoid ABCD, in which the following holds: AB= 6cm, Area of triangle ABC= 15 cm2, area of triangle BCD= 20 cm2, AB||CD. - Arbor
 Calculate in square meters the area of an arbor whose ground plan is in the shape of a regular hexagon with a side length of 4.5 m.
Calculate in square meters the area of an arbor whose ground plan is in the shape of a regular hexagon with a side length of 4.5 m. - Resulting cross
 From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross?
From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross? - A yard
 Yevgen is fencing in a yard that is 30 meters longer than it is wide. The yard will have an area of 1000 m². Find its width and length.
Yevgen is fencing in a yard that is 30 meters longer than it is wide. The yard will have an area of 1000 m². Find its width and length. - Baking a cake
 Christy is baking a cake that has a 9-inch diameter. She wants to cover the top of the cake with buttercream icing. How much icing will she need?
Christy is baking a cake that has a 9-inch diameter. She wants to cover the top of the cake with buttercream icing. How much icing will she need? - A square 3
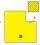 A square (with side b=2ft) is removed from the right-hand corner of a square board with side a= 12 ft. What is the area of the remaining board in square feet?
A square (with side b=2ft) is removed from the right-hand corner of a square board with side a= 12 ft. What is the area of the remaining board in square feet? - The length 8
 The length of a rectangular field is x + 4, and its width is x + 2. What is the area of the field? Answer in polynomials expressions.
The length of a rectangular field is x + 4, and its width is x + 2. What is the area of the field? Answer in polynomials expressions. - Four sides of trapezoid
 Calculate the area of the ABCD trapezoid with sides a = 65 cm, b = 29 cm, c = 40 cm, d = 36 cm
Calculate the area of the ABCD trapezoid with sides a = 65 cm, b = 29 cm, c = 40 cm, d = 36 cm - The ABCD
 The ABCD trapezoid has a base length of a = 120mm, c = 86mm, and an area of S = 2575 mm². Calculate the height of the trapezoid.
The ABCD trapezoid has a base length of a = 120mm, c = 86mm, and an area of S = 2575 mm². Calculate the height of the trapezoid. - Length 7
 Length equals 7/6 inch in width equals 7/9 inches the area is?
Length equals 7/6 inch in width equals 7/9 inches the area is? - Compressive force
 The excavator's area of belts is 5 m2, and it creates a pressure of 40 kPa. How much compressive force does the excavator exert on the road?
The excavator's area of belts is 5 m2, and it creates a pressure of 40 kPa. How much compressive force does the excavator exert on the road? - Parallerogram
 The ABCD parallelogram is a = 2.5 cm, height to side a is 7.2 cm and height to side b is 4 cm. Find the side length b.
The ABCD parallelogram is a = 2.5 cm, height to side a is 7.2 cm and height to side b is 4 cm. Find the side length b. - Is right triangle or not
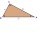 If the right triangle is ABC, it has sides a=13, b=11.5, and c=22.5. Find area.
If the right triangle is ABC, it has sides a=13, b=11.5, and c=22.5. Find area. - Enlarged rectangle
 The rectangle has dimensions of 8 cm and 12 cm. We enlarge it in a ratio of 5:4. What are the circumference and the area of the enlarged rectangle?
The rectangle has dimensions of 8 cm and 12 cm. We enlarge it in a ratio of 5:4. What are the circumference and the area of the enlarged rectangle? - Square
 Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm².
Square JKLM has sides of a length of 24 cm. Point S is the center of LM. Calculate the area of the quadrant JKSM in cm². - Diameters of circles
 How many percent of the area of a larger circle is a smaller circle if the smaller circle has a diameter of 120 mm and a larger one has a diameter of 300 mm?
How many percent of the area of a larger circle is a smaller circle if the smaller circle has a diameter of 120 mm and a larger one has a diameter of 300 mm?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
