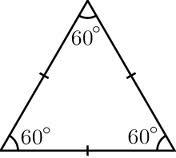
Equilateral triangle
Calculate the side of an equilateral triangle if its area is 886 mm2.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Equilateral 80573
The field has the shape of an equilateral triangle. Calculate its area if you know that the side is 280 meters long. - Cross-section 47131
The 5 m long bar has a cross-section of an equilateral triangle with a side of 35 mm. Calculate its volume - Equilateral 81770
Calculate the area of the circle in which the hole is cut in the shape of an equilateral triangle when the diameter of the circle, d=32mm, and the side of the triangle, a=20.8mm. - Calculate 4215
Calculate the length of the side of the rectangle if you know its perimeter and the other side: a) o = 100 m: b = 2.5 m b) o = 80 cm: a = 20 mm c) o = 38.6 dm: b = 45 cm d) o = 88 mm: a = 2.5 cm
- Equilateral triangle v2
Calculate the side of an equilateral triangle if its perimeter is 132 cm. - Equilateral 2543
a) The perimeter of the equilateral triangle ABC is 63 cm. Calculate the side sizes of the triangle and its height. b) A right isosceles triangle has an area of 40.5 square meters. How big is his circuit? c) Calculate the square's area if the diagonal's s - Equilateral triangle
The equilateral triangle has a 23 cm long side. Calculate its area.
