Practice problems of the area of an angle
Number of problems found: 257
- The apothem
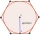 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - One side 4
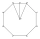 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - Consecutive Interior Angles
 PQRS is a trapezium in which PQ is parallel to SR and ∠P = 130 ̊, ∠Q = 110 ̊. Find the remaining angles.
PQRS is a trapezium in which PQ is parallel to SR and ∠P = 130 ̊, ∠Q = 110 ̊. Find the remaining angles. - Calculate 83261
 Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3
- Overhangs 83158
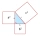 The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b.
The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b. - Calculate 82696
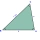 In the triangle ABC, b=5 cm, c=6 cm, /BAC/ = 80° are given. Calculate the sizes of the other sides and angles, and further determine the sizes of the tangent tc and the area of the triangle.
In the triangle ABC, b=5 cm, c=6 cm, /BAC/ = 80° are given. Calculate the sizes of the other sides and angles, and further determine the sizes of the tangent tc and the area of the triangle. - Calculate 82567
 The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area.
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - Circular 82418
 A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius?
A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius? - Quadrilateral 82146
 Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base.
Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base.
- Determine 82032
 Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base. - Right-angled 81989
 Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8
Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8 - Calculate 81950
 The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle.
The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle. - Revolutions 81906
 How much energy was supplied by the flywheel of the device if its number of revolutions decreased from 1200 to 720 revolutions per minute if it has a moment of inertia of 71.3 kg/m²?
How much energy was supplied by the flywheel of the device if its number of revolutions decreased from 1200 to 720 revolutions per minute if it has a moment of inertia of 71.3 kg/m²? - Circumscribed 81759
 In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle.
In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle.
- Calculate 81757
 Calculate the size of the largest angle in triangle ABC if a = 7 cm, b = 8 cm, and c = 13 cm. Calculate the area of the triangle, the height per side a.
Calculate the size of the largest angle in triangle ABC if a = 7 cm, b = 8 cm, and c = 13 cm. Calculate the area of the triangle, the height per side a. - Determine 81756
 The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base.
The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base. - Intersection 81594
 Given a trapezoid ABCD and the sizes of the interior angles. Angle SDC 32° SAD angle 33° SDA angle 77° Angle CBS 29°, where S is the intersection of the diagonals. What is the size of the angle BSA?
Given a trapezoid ABCD and the sizes of the interior angles. Angle SDC 32° SAD angle 33° SDA angle 77° Angle CBS 29°, where S is the intersection of the diagonals. What is the size of the angle BSA? - Archaeologists 81478
 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Perpendicular 81381
 Which parking lot for 5 cars occupies a larger area, perpendicular or inclined at an angle of 45°, and how much? the car has dimensions of 4m and 2m.
Which parking lot for 5 cars occupies a larger area, perpendicular or inclined at an angle of 45°, and how much? the car has dimensions of 4m and 2m.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
