Cube practice problems - page 24 of 28
Number of problems found: 559
- Circumscribed - sphere
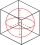A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere. - Cutting the prism
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - Ball diameter density
What is the diameter of the ball (for men) if it weighs 7,250 g and ρ = 7.8g / cm³ - Cube surface area
What is the largest surface area of a square glued together from 12 identical cubes with an edge length of 1 cm? - Equilateral cylinder
The equilateral cylinder (height = base diameter; h = 2r) has a V = 178 cm³ volume. Calculate the surface area of the cylinder. - Wrapping box
Will you need more paper to wrap a 2.3dm cube box or a 12 cm, 3 dm, and 8 cm cube-shaped box? - Pyramid stone weight
The largest Egyptian pyramid has the shape of a regular four-sided pyramid with a base edge of approximately 227 meters and a height of about 140 meters. How many tons of stone did the workers transport to build it? One cube of stone weighs 2500 kg and ne - Radius of a sphere
We turned a sphere with the largest possible radius from a cube with an edge length of 8 cm. Calculate the volume of the cube, the ball, and the percentage of waste when turning. - Special body
Above each wall of a cube with an edge a = 30 cm, we construct a regular quadrilateral pyramid with a height of 15 cm. Find the volume of the resulting body. - Diagonal of a cube Calculate the volume of a cube with a wall diagonal of u = 20 cm.
- Sphere cube percentage
A sphere is placed inside the 10 cm cube to touch all the cube's walls. What percentage of the volume of a cube makes up the volume of a sphere? - Pyramid cut
We cut the regular square pyramid with a parallel plane to the two parts (see figure). The volume of the smaller pyramid is 20% of the volume of the original one. The bottom of the base of the smaller pyramid has an area of 10 cm². Find the area of the or - Thousand balls
We must create a thousand balls from a sphere with a diameter of 1 m. What will be their radius? - Sphere radius calculation
Calculate the radius of a sphere with a volume of 6.2 dm3, round to the nearest centimeter. - Cube in ball
The cube is inscribed into the sphere of radius 6 dm. How many percent is the volume of the cube of the volume of the sphere? - Cubes
One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm². - Cube into sphere
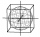The cube has brushed a sphere as large as possible. Determine how much percent the waste was. - Cube into cylinder
If we dip a wooden cube into a barrel with a 40cm radius, the water will rise 10 cm. What is the size of the cube edge? - Cube surface
Calculate the cube's surface with the edges of the length: 2 half cm, 3.5 cm; it is a quarter of a cm. - Ball box percentage A ball with a diameter of 10 cm is in a cube-shaped box with an edge of 10 cm. What percentage of the box does the ball fill?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
