Cutting the prism
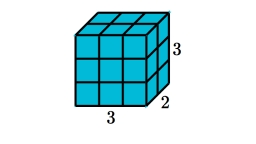
A prism with a square base with an area of 1 cm2 and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism?
Final Answer:
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Triangular prism
The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The area of the largest sidewall of its surface is 130 cm², and the body's height is 10 cm. Calculate its volume. - Prism surface
The base of the vertical prism is a right triangle with a perpendicular 5 cm. The area of the largest wall is 130 cm2, and the body's height is 10 cm. Calculate the surface area of the body. - Prism pyramid volume
Calculate the body's volume, consisting of a prism and a pyramid with the same square base with an edge of 8 cm. The prism is 20 cm high, and the pyramid is 15 cm. - Cube corners
We cut a small cube with an edge length of 2 cm from each corner of a large cube with an edge length of 10 cm. How many cm³ was the body left from the big cube after cutting the small cubes? - Regular square prism
The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism. - Regular triangular prism
Calculate the surface area of the body of a regular triangular prism when the length of its base edge is 6.5 cm, and its height is 0.2 m. - Cylinder hole
A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of
