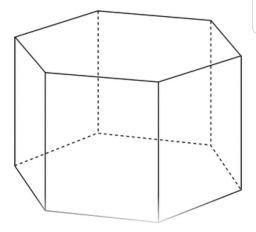
Hexagonal prism volume
A perpendicular hexagonal prism was created by machining a cube with an edge length of 8 cm. The base of the prism is created from the square wall of the original cube by separating 4 identical right triangles with overhangs of lengths 3cm and 4cm. The height of the prism is 8 cm. What is the volume of a hexagonal prism
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Right triangle prism
 The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle.
The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle. - Cutting the prism
 A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism?
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - Hexagon, hexa S, V
 What is the surface area and volume of a regular hexagonal prism with a base edge of 12cm and a height of the prism equal to the diameter of the circle circumscribed by the base?
What is the surface area and volume of a regular hexagonal prism with a base edge of 12cm and a height of the prism equal to the diameter of the circle circumscribed by the base? - Hexagonal prism volume
 Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm.
Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm. - Hexagonal prism
 The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism. - Base of prism
 The base of the perpendicular prism is a rectangular triangle whose legs lengths are at a 3:4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm².
The base of the perpendicular prism is a rectangular triangle whose legs lengths are at a 3:4 ratio. The height of the prism is 2cm smaller than the larger base leg. Determine the volume of the prism if its surface is 468 cm². - Hexagonal wax
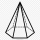 The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax.
The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax.
