Hranol
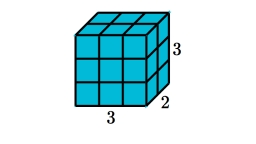
Z kocky s dĺžkou hrany 3 cm bol vyrezaný hranol s štvorcovou podstavou o obsahu 1 cm2 a výškou 3 cm. Aký je povrch telesa, ktoré z kocky vzniklo po vyrezanie hranola?
Vaša odpoveď:
Vaša odpoveď:
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Kváder 50
Kváder so štvorcovou podstavou dĺžkou hrany 4 dm má povrch 112 dm štvorcových. Urč jeho výšku. - Rovnostranný - hranol
Vypočítajte objem a povrch hranola s výškou 9,6 cm s podstavou rovnostranného trojuholníka s dĺžkou 4,8 cm. - Hranol s ihlanom
Vypočítajte objem telesa, ktoré je zložené z hranola a ihlana s rovnakou štvorcovou podstavou s hranou 8 cm. Hranol je vysoký 20 cm a ihlan 15 cm. - Hranoly 2
Otázka č.1: Hranol má rozmery a=2,5 cm, b=100 mm, c=12 cm. Aký je jeho objem? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Otázka č.2: Podstava hranola je kosoštvorec s dĺžkou strany 30 cm a výškou 27 cm. Výška hranola je 5 dm. Aký je objem hranola? a) 2 - Vypočítajte 258
Vypočítajte objem a povrch hranola s lichobežníkovou podstavou a výškou 9 cm. Podstava je rovnoramenný lichobežník so základňami s dĺžkami 3 cm a 6 cm a ramenami dĺžky 2,5 cm. Výška podstavy je 2 cm. - Plášť hranola
Vypočítaj povrch hranola so štvorcovou podstavou ktorého plášt je obdĺžnik so stranami 18 cm a 8 cm. Koľko riešeni má úloha? Uved všetky riešenia. - Hračkárske kocky
Z detských drevených kociek tvaru hranola so štvorcovou podstavou (strana podstavy je 4 cm dlhá, výška hranola je 8 cm) je postavená pevnosť s vežami z dvoch kociek nad sebou zakončenými ihlanmi s rovnakou podstavou ako hranolmi a výškou 6 cm. Všetky sten
