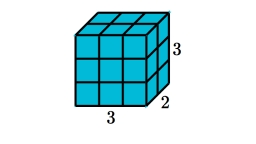
Po vyříznutí hranolu
Z krychle s délkou hrany 3 cm byl vyříznut hranol s čtvercovou podstavou o obsahu 1 cm2 a výškou 3 cm. Jaký je povrch tělesa, které z krychle vzniklo po vyříznutí hranolu?
Vaše odpověď:
Vaše odpověď:
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Rohy kostky
Z každého rohu velké kostky s délkou hrany 10 cm byla vyříznuta malá kostka s délkou hrany 2 cm. Kolik cm³ mělo těleso, které zůstalo z velké kostky po vyříznutí malých kostek? - Čtvereční podstava
Kvádr se čtvercovou podstavou délkou hrany 4 dm má povrch 112 dm čtverečních. Urč jeho výšku. - Hranoly
Otázka č.1: Hranol má rozměry a = 2,5 cm, b = 100 mm, c = 12 cm. Jaký je jeho objem? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Otázka č.2: Podstava hranolu je kosočtverec s délkou strany 30 cm a výškou 27 cm. Výška hranolu je 5 dm. Jaký je objem hrano - Hranol + jehlan
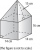Vypočítejte objem tělesa, které je složeno z hranolu a jehlanu se stejnou čtvercovou podstavou o hraně 8 cm. Hranol je vysoký 20 cm a jehlan 15 cm. - Úhlopříčka
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60 stupňů, délka hrany postavy je 10 cm. Jaký je objem tělesa? - Povrch hranolu
Vypočítej povrch hranolu se čtvercovou podstavou jehož plášt je obdélník se stranami 18 cm a 8 cm. Kolik řešení má úkol? Uveďte všechna řešení. - Vypočítejte 258
Vypočítejte objem a povrch hranolu s lichoběžníkovou podstavou a výškou 9 cm. Podstava je rovnoramenný lichoběžník se základnami o délkách 3 cm a 6 cm a rameny délky 2,5 cm. Výška podstavy je 2 cm.
