Průnik množin - příklady
Počet nalezených příkladů: 198
- Dopravních 84293
Z celkového počtu dopravních nehod se 80% stane v obci a 20% mimo obec. Kdyby se podařilo snížit počet dopravních nehod v obci o 40%, o kolik procent by klesl celkový počet dopravních nehod? - ZUŠ - hudba
Hudební a výtvarný obor v základní umělecké škole navštěvuje 86 žáků. Hudební obor navštěvuje 45 žáků, výtvarný obor navštěvuje 53 žáků. Několik žáci navštěvují oba obory. Kolik žáků navštěvuje hudební a výtvarný obor zároveň? - Střelec 6
Střelec se trefí do terče s pravděpodobností 78 %. Určete, s jakou pravděpodobností se při soutěži, kdy se střílí 3 rány po sobě, netrefí pouze při první ráně. Výsledek zaokrouhlete na dvě desetinná místa. - Alespoň 83951
Ze 124 žáků šlo alespoň na jeden ze dvou výletů 68 žáků. Na první vylet nešlo 82 žáků, 63 žáků šlo právě na jeden vylet. Kolik žáků šlo pouze na první vylet, kolik žáků šlo na druhý vylet? - Občerstvení
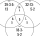Na taneční party byly k občerstvení připraveny chlebíčky, kofola a zákusky. 18 lidí jídlo zákusky, 29 lidí chlebíčky a kofolu pilo 32 lidí. Dva lidé nezkonzumovali ani jeden druh občerstvení. Všechny druhy mělo 5 lidí. Kofolu a zákusky mělo 7 lidí, chlebí - Souřadnice bodu
Mám bod A=[2,1] a přímku y+x-5=0. Jak určím souřadnice bod A´, který je obrazem bodu A podle dané přímky? - Obdélníkový 83244
Obdélníkový bazén má rozměry 25 metrů a 12,5 metru. Kolem bazénu je stezka široká 2 metry. Kolik metrů čtverečních dlaždic je potřeba k vydláždění chodníku?
- Zvířátka 83223 Ve třídě je 24 žáků. psa má doma 11 z nich. Drobného hlodavce má 15 z nich. Žádné zvířátko nemá doma 5 žáků. Kolik žáků má doma 2 zvířátka?
- Společný bod
Určete hodnotu čísla a tak, aby grafy funkcí f: y = x² a g: y = 2x + a měly společný právě jeden bod. - Průsečíky - parametricky
Vypočtěte součet x-ových souřadnic průsečíků kružnice dané rovnicí (x - 1)²+ y² = 1 a přímky dané parametricky x = t, y = t , kde t∈R. - Do kroužku Do kroužku chodí 29 dětí. 11 uvedlo, že má doma psa, 14 dětí má doma kočku a 12 dětí má doma křečka. Dvě děti mají všechna tři zvířátka. 7 dětí nemá doma žádné zvíře. . Kolik dětí má alespoň dvě z uvedených zvířat? Kolik dětí má právě jedno z uvedených zv
- Klimatizovaných 82383
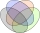Autosalon prodává automobily - několik značek. Za poslední měsíc bylo prodáno celkem 61 vozů. Automobilů vybavených klimatizací bylo prodáno třikrát více, než automobilů značky Škoda. Automobilů Škoda, které nebyly vybaveny klimatizací, bylo prodáno o 6 m - Zaměstnanců 82035 V době krádeže bylo v hotelu 96 lidí, 61 z nich je mimo podezření. Ze 47 zaměstnanců, kteří byli v hotelu, je 23 mimo podezření. Kolik hostů není mimo podezření?
- Sedadla v kině
Vypočítejte pravděpodobnost události, že si v kině na sedadlech 1 až 30 sednete na: a) sedadlo označené prvočíslem b) sedadlo označené sudým číslem c) sedadlo označené číslem dělitelným 3 nebo 4 - Ortocentrum
Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran.
- Hodíme 4
Hodíme třikrát kostkou. Vypočítejte pravděpodobnost, že při prvním, nebo druhém, nebo třetím hodu padne sudé číslo. - 200 studentů 200 studentů dělalo zkoušky z češtiny, matematiky a fyziky. 114 studentů udělalo češtinu, 50 studentů udělalo matematiku a 41 studentů udělalo fyziku. Zkoušku z češtiny i matematiky udělalo 14 studentů, z matematiky i fyziky 15 studentů a z češtiny i fyzi
- Anketa Anketa, provedená u 200 studentů jedné školy, zjišťovala, který ze zpěváků V. Neckář, K. Gott, W. Matuška je nejvíce oblíben. Přinesla tyto výsledky: Gott je oblíben u 78 studentů, Matuška u 75 studentů a Neckář u 101. Dále se zjistilo, že všichni tři jso
- Klub důchodců
Klub důchodců uspořádal sběr léčivých rostlin. Dva důchodci se ze zdravotních důvodů nemohli sběru zúčastnit, ostatní se rozhodli sbirat hluchavku, bez a podběl. Všechny tři byliny sbíralo 7 důchodců, hluchavku i bez 15 důchodců, hluchavku i podběl 12 důc - Ze 32 Ze 32 lidí jich 22 má rádo ryby. Na houbách si rádo pochutná o 4 osoby méně. Těch, kteří jí houby nebo ryby, je 7krát více než těch, kteří houby ani ryby nejedi. Kolik z dotázaných ji ryby i houby?
Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
Viz také více informacií na Wikipedii.
