Ortocentrum
Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran.
Vaše odpověď:
Vaše odpověď:
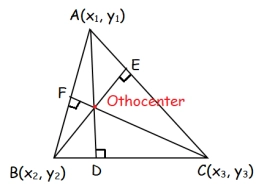
Tipy na související online kalkulačky
Základem výpočtů v analytické geometrii je dobrá kalkulačka rovnice přímky, která ze souřadnic dvou bodů v rovině vypočítá smernicový, normálový i parametrický tvar přímky, směrnici, směrový úhel, směrový vektor, délku úsečky, průsečíky se souřadnicovým osami atd.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraplanimetrieÚroveň náročnosti úkolu
Související a podobné příklady:
- Lineární funkce
Zapiš zda je funkce rostoucí nebo klesající a urči souřadnice průsečíku s osami x a y: y=3x-2 y=5x+5 y=-0,5x-1 - Průsečík s osou y
Jaký je průsečík osy y s přímkou 4x + 8y = 16? Napište souřadnice x0, y0 tohoto průsečíku osy y. - Souřadnice - úsečka V jakém poměru je úsečka spojující P (5, 3) a Q (–5, 3) dělená osou y? Najděte také souřadnice průsečíku.
- Čtverec - geometria
V pravoúhlé soustavě souřadnic je dán bod A[-2;-4] a bod S[0;-2]. Urči souřadnice bodu B, C, D tak, aby ABCD byl čtverec a S prusečik jejich uhlopřiček. - Souřadnice průsečíků
Jaký je součet všech souřadnic bodů, které jsou průsečíky přímky p: x = -1-2t, y = 5-4t, z = -3+6t, kde t je reálné číslo, se souřadnicovými rovinami xy a yz? - Souřadnice těžiště
Nechť A = [3, 2, 0], B = [1, -2, 4] a C = [1, 1, 1] jsou 3 body v prostoru. Vypočítejte souřadnice těžiště △ ABC (je to průsečík těžnic). - Je dána 6
Je dána kvadratická funkce: y=-x²+2x+3 a) urči průsečíky s osou x, y a vrchol V b) načrtni graf a popiš c) pro které x platí f(x)=3
