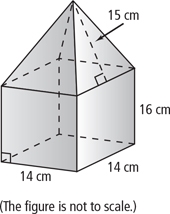
Prism pyramid volume
Calculate the body's volume, consisting of a prism and a pyramid with the same square base with an edge of 8 cm. The prism is 20 cm high, and the pyramid is 15 cm.
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Triangular prism
 The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The area of the largest sidewall of its surface is 130 cm², and the body's height is 10 cm. Calculate its volume.
The base of the perpendicular triangular prism is a right triangle with a leg length of 5 cm. The area of the largest sidewall of its surface is 130 cm², and the body's height is 10 cm. Calculate its volume. - Cutting the prism
 A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism?
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - Prism surface
 The base of the vertical prism is a right triangle with a perpendicular 5 cm. The area of the largest wall is 130 cm2, and the body's height is 10 cm. Calculate the surface area of the body.
The base of the vertical prism is a right triangle with a perpendicular 5 cm. The area of the largest wall is 130 cm2, and the body's height is 10 cm. Calculate the surface area of the body. - The cast
 The cast in the body of a regular quadrilateral pyramid with a base edge 60 cm long and 5 cm high is made of a material with a density of 7.8 g/cm cubic. Calculate its weight.
The cast in the body of a regular quadrilateral pyramid with a base edge 60 cm long and 5 cm high is made of a material with a density of 7.8 g/cm cubic. Calculate its weight. - Quadrilateral prism
 The body diagonal of a regular quadrilateral prism forms an angle of 60° with the base. The edge of the base is 20 cm long. Calculate the volume of the body.
The body diagonal of a regular quadrilateral prism forms an angle of 60° with the base. The edge of the base is 20 cm long. Calculate the volume of the body. - Prism volume
 Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5
Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5 - Cylinder hole
 A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of
A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of
