Equations practice problems - page 38 of 241
Number of problems found: 4814
- Worker reward division
The reward of CZK 4,220 was divided among 3 workers in such a way that the second received CZK 400 more than the first, and the third received 30% more than the second. How much did each get? - Equation of a circle
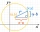Write the general equation of a circle with center S(2;5) and point B(5;6) lying on this circle. - Karel Ondra pursuit
Karel went for a walk at a speed of 5 km/h. After 3 hours, Ondra rode to him with an important message. He was moving at a speed of 20 km/h. How many minutes did Ondra catch up with Karel? - Unknown number calculation
I divide the unknown number by 2 and then add 4 to the result, which gives me 22. What is the unknown number? - Forester sapling planting
Foresters planted 2,440 saplings in three days. On the second day, they planted 20% more saplings than on the first day, and on the third day, 15% less than on the first day. How many saplings did the foresters plant each day? - Water lily colors
There are twice as many pink water lilies in the pond as yellow water lilies, but twice as few as white water lilies. Which water lilies are the most and which are the fewest? How many times more white water lilies are there than yellow water lilies? How - Margaret savings gifts
Margaret bought Christmas presents with a quarter of her savings. How much did she save if the gifts cost CZK 160? Express the rest of the savings as a fraction. - Geometric sequence terms
The two terms of the geometric sequence are a2=12 and a5=three halves. a) calculate the tenth term of the sequence. b) calculate the sum of the first 8 terms of the sequence. v) how many first terms of the sequence need to be added so that the sum is equa - Martin age years
Martin will be twice as old in 10 years as he was four years ago. How old is she now? - Arithmetic geometric sequence Determine four numbers so that the first three form the successive three terms of an arithmetic sequence with difference d=-3 and the last three form the next terms of a geometric sequence with quotient q=one half.
- Jane ring money
Jane lacked 160 crowns to buy six rings, so she only bought four and had 100 crowns left. How much are 4 rings? - Cottage bridge distance
Two neighboring cottagers have cottages under the forest by the stream. They decided to build a bridge over the stream at a place far from the two huts. The distance between the cottages is 230 m; one cottage is 120 m from the stream, and the other is 85 - Ema picture cards
Ema has 3 times more picture cards in her collection than Dana. They have a total of 240 images. They are bought in packs of 10 for CZK 14. How much did Dana's pictures cost? - Athletics
160 students (gymnasiums and technical schools) participated in the athletics race. The proportion of girls from the gymnasium was 50%, the proportion of girls from the technical schools was 10%. Determine how many students were from the gymnasiums and ho - Arithmetic sequence indices In which arithmetic sequence is the sum of the first five terms with odd indices equal to 85 and the sum of the first five terms with even indices equal to 100?
- Jude section children Three times more boys than girls go to the Jude section. If three more girls started dating, there would be twice as many boys as girls. A) determine how many go to the girls' section B) determine how many children attend the department in total.
- Arithmetic sequence middle An increasing arithmetic sequence has an odd number of terms. The middle term is 302. If we remove the 4 largest terms from the sequence, the middle term will be 296. Determine the difference in the sequence.
- Mobile phone minutes
Mr. Hovorka pays a monthly flat rate of CZK 100 plus CZK 0.90 for each started minute of the call for his mobile phone. He calculated that each minute of the call last month cost him CZK 2.15. How many minutes was he on the phone? - Sequence sum formula Two arithmetic sequences have the same first term. The nth term of the first sequence is 15, and of the second sequence, 21. The sum of the first n terms of the first sequence is 63, and of the second sequence, 84. Write the sums of the first n terms of b
- Geometric series terms
The sum of the first two terms of the descending geometric sequence is five quarters, and the sum of the infinite geometric series formed from it is nine quarters. Write the first three terms of the geometric sequence.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
