Geometric series terms
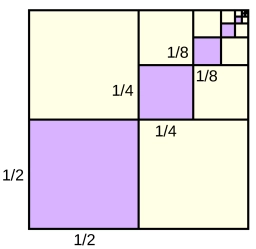
The sum of the first two terms of the descending geometric sequence is five quarters, and the sum of the infinite geometric series formed from it is nine quarters. Write the first three terms of the geometric sequence.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Need help calculating a sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Need help calculating a sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetrybasic operations and conceptsnumbersGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Sum of GP members
Determine the sum of the GP 30, 6, 1.2, to 5 terms. What is the sum of all terms (to infinity)? - Specific series
Write the next three terms of the series formed according to a specific rule: 1, √2, 9, 2, 25, …, …, … - Geometric series
How many terms of the geometric series 8+4+2+1+0.5+... must be taken for the sum to get within 10 to the power minus 4 of its sum to infinity? - Geometric sequence sum Determine s5 of the geometric sequence if: a1 + a2 = 10 and a4 - a2 = 120
- Geometric sequence calculation
Determine the remaining quantities in the finite geometric sequence, given: n = 4, an = 12.5, sn = 187.5, a1 = ?, q =? - Infinite series
Determine the sum of an infinite series: 1/3 + 1/9 + 1/27 + 1/81 ... - Fraction
Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator.
