Isolating a variable in the formula + sphere - practice problems
Number of problems found: 19
- Surface = volume
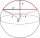 If the volume and the surface area of a sphere are numerically the same then find its radius.
If the volume and the surface area of a sphere are numerically the same then find its radius. - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Calculate 81034
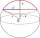 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm. - Sphere - diameter
 What is the diameter of a 1m³ sphere? Write in decimetres
What is the diameter of a 1m³ sphere? Write in decimetres
- One-quarter 46001
 Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm.
Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm. - Sphere cut
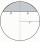 A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Sphere in cone
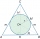 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Ball-shaped 28481
 How many square meters of material is needed to make a ball-shaped balloon with a volume of 950 m³?
How many square meters of material is needed to make a ball-shaped balloon with a volume of 950 m³? - Spherical segment
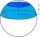 Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm.
Calculate the volume of a spherical segment 18 cm high. The diameter of the lower base is 80 cm, and the upper base is 60 cm.
- Two hemispheres
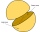 In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)?
In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)? - Sphere-shaped 20723
 The sphere-shaped reservoir has a volume of 282 hl. Calculate the material consumption in m² for its production, assuming 8% for joints and waste, and round the final result to the nearest total.
The sphere-shaped reservoir has a volume of 282 hl. Calculate the material consumption in m² for its production, assuming 8% for joints and waste, and round the final result to the nearest total. - Tropics and polar zones
 What percentage of the Earth's surface lies in the tropical, temperate, and polar zones? Tropics border individual zones at 23°27' and polar circles at 66°33'.
What percentage of the Earth's surface lies in the tropical, temperate, and polar zones? Tropics border individual zones at 23°27' and polar circles at 66°33'. - Truncated cone and sphere
 A sphere is inscribed in a truncated cone with base diameters D1=10 cm and D2=20 cm, touching both bases and the surface. What is its diameter?
A sphere is inscribed in a truncated cone with base diameters D1=10 cm and D2=20 cm, touching both bases and the surface. What is its diameter? - Pebble
 The aquarium is filled with two-thirds water with internal dimensions of the bottom 40 cm × 35 cm and a height of 30 cm. Calculate how many millimeters the water level in the aquarium rises by dipping a pebble-shaped sphere with a diameter of 18 cm.
The aquarium is filled with two-thirds water with internal dimensions of the bottom 40 cm × 35 cm and a height of 30 cm. Calculate how many millimeters the water level in the aquarium rises by dipping a pebble-shaped sphere with a diameter of 18 cm.
- Diameter 7648
 The mug has the shape of a cylinder with a height of 60.7 mm. There is two dl of water in it. If we dip a ball with a diameter of 40 cm into the water, the water will not overflow. What is the minimum diameter of the cup?
The mug has the shape of a cylinder with a height of 60.7 mm. There is two dl of water in it. If we dip a ball with a diameter of 40 cm into the water, the water will not overflow. What is the minimum diameter of the cup? - MO SK/CZ Z9–I–3
 John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball. - Billiard balls
 A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original.
A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original. - Spherical segment
 The spherical segment with height h=2 has a volume of V=225. Calculate the radius of the sphere which is cut in this segment.
The spherical segment with height h=2 has a volume of V=225. Calculate the radius of the sphere which is cut in this segment. - Cube in a sphere
 The cube is inscribed in a sphere with a volume 8101 cm³. Determine the length of the edges of a cube.
The cube is inscribed in a sphere with a volume 8101 cm³. Determine the length of the edges of a cube.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
