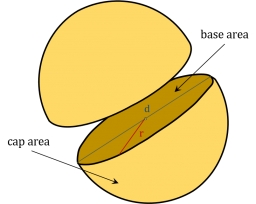
Two hemispheres

In a wooden hemisphere with a radius r = 1, a hemispherical depression with a radius r/2 was created so that the bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)?

Correct answer:

S =  10.2102 cm²

Step-by-step explanation:

$$\begin{gathered} r=1 \\ {r}_2=r\mathrm{/}2=1\mathrm{/}2={\displaystyle \frac{1}{2}}=0.5 \\ {S}_1=\pi \cdot r^2=3.1416\cdot 1^2\doteq 3.1416 \\ {S}_2=\pi \cdot r_2^2=3.1416\cdot 0.5^2\doteq 0.7854 \\ {S}_{11}=4\pi \cdot r^2\mathrm{/}2=4\cdot 3.1416\cdot 1^2\mathrm{/}2\doteq 6.2832 \\ {S}_{22}=4\pi \cdot r_2^2\mathrm{/}2=4\cdot 3.1416\cdot 0.5^2\mathrm{/}2\doteq 1.5708 \\ S=S_{11}+S_{22}+S_1-S_2=6.2832+1.5708+3.1416-0.7854\doteq 10.2102 \\ \text{ Verifying Solution: } \\ q=S\mathrm{/}\pi \mathrm{/}{r}^2=10.2102\mathrm{/}3.1416\mathrm{/}{1}^2={\displaystyle \frac{13}{4}}=3.25 \\ S={\displaystyle \frac{13}{4}}\cdot \pi \cdot r^2=10.2102{\text{cm}}^2 \end{gathered}$$

Try another example

Related math problems and questions:

• Spherical cap
  Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which the spherical cap was cut.
• Spherical cap
  From the sphere of radius 11 was truncated spherical cap. Its height is 6. What part of the volume is a spherical cap from the whole sphere?
• Sphere cut
  A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
• Spherical cap 4
  What is the surface area of a spherical cap, the base diameter 20 m, height 2.5 m? Calculate using formula.
• Sphere - parts
  Calculate the area of a spherical cap, which is part of an area with base radius ρ = 9 cm and a height v = 3.1 cm.
• Spherical segment
  The spherical segment with height h=1 has a volume V=223. Calculate the radius of the sphere of which is cut this segment.
• Hemisphere cut
  Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm.
• Spherical cap
  The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut.
• Sphere parts, segment
  A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. .What are the volume of the segment and the surface of the segment?
• Sphere A2V
  The surface of the sphere is 241 mm². What is its volume?
• Sphere cuts
  At what distance from the center intersects sphere with radius R = 56 plane, if the cut area and area of the main sphere circle is in ratio 1/2.
• Spherical cap
  What is the surface area of a spherical cap, the base diameter 20 m, height 2 m.
• The volume
  The volume of the sphere is 1 m³, what is its surface?
• Eight
  Eight small Christmas balls with a radius of 1 cm have the same volume as one large Christmas ball. What has a bigger surface: eight small balls, or one big ball?
• A spherical segment
  A spherical section whose axial section has an angle of j = 120° in the center of the sphere is part of a sphere with a radius r = 10 cm. Calculate the cut surface.
• Above Earth
  To what height must a boy be raised above the earth to see one-fifth of its surface.
• Hemispherical hollow
  The vessel hemispherical hollow is filled with water to a height of 10 cm =. How many liters of water are inside if the hollow's inside diameter is d = 28cm?