Spherical cap practice problems

A spherical cap (or spherical segment) is the portion of a sphere cut off by a plane. It resembles a "cap" on top of the sphere.

Instructions: Take your time with each problem and write out how you solved it step by step.

Number of problems found: 43

Tent - spherical cap
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
Spherical section cut
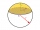Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
Spherical cap 4
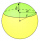What is the surface area of a spherical cap, the base diameter of 20 m, and the height of 2.5 m? Calculate using the formula.
Spherical cap
What is the surface area of a spherical cap, the base diameter 27 m, and height 2 m?
MO SK/CZ Z9–I–3
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
Spherical tank
The water tower tank is a sphere with a radius of 35ft. If the tank is filled to one-quarter full, what is the height of the water?
Float boya
A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³.
Two Sections
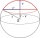A sphere with a radius of 5 cm was divided into two spherical sections. The height of the smaller section is 1cm. Determine the volume of the smaller section to the nearest hundredth of a cm³.
Big Earth
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km.
Felix
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Tropical, mild and arctic
How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'.
Elevation
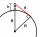What must be an observer's elevation so that he may see an object on the Earth 866 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
Tropics and polar zones
What percentage of the Earth's surface lies in the tropical, temperate, and polar zones? Tropics border individual zones at 23°27' and polar circles at 66°33'.
A plane vs. sphere
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
The roof
The roof has a spherical canopy with a base diameter of 8 m and a height of 2 m. Calculate the foil area with which the roof is covered when calculating 13% for waste and residues.
Sphere - parts
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm.
Spherical cap
From the sphere with a radius of 26 was a truncated spherical cap. Its height is 2. What part of the volume is a spherical cap from the whole sphere?
Above Earth
To what height must a boy be raised above the earth to see one-fifth of its surface?
Spherical cap
The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut.
Airplane
Aviator sees part of the earth's surface with an area of 200,000 square kilometers. How high does he fly?

Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.