Pythagorean theorem + spherical cap - practice problems
Number of problems found: 23
- MO SK/CZ Z9–I–3
 John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The diameter of the circle that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The diameter of the circle that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball. - What percentage
 What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km.
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km. - Float boya
 A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³.
A 0.5-meter spherical float is a location mark for a fishing boat anchor. It floats in salt water. Find the depth to which the float sinks if the material of which the float is made weighs 8 kilograms per cubic meter and saltwater weighs 1027 kg/m³. - Felix
 Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
- Dimensions: 32561
 The convex lens consists of two spherical segments (dimensions given in mm). Calculate its weight if the density of the glass is 2.5 g/cm³. Dimensions: 60mm in length and width of the upper part 5mm, the width of the lower part 8mm
The convex lens consists of two spherical segments (dimensions given in mm). Calculate its weight if the density of the glass is 2.5 g/cm³. Dimensions: 60mm in length and width of the upper part 5mm, the width of the lower part 8mm - Calculate 81034
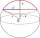 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm. - Spherical 63214
 The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca
The gas tank consists of a 16m high cylinder with a diameter of 28m, which is closed at the top by a spherical canopy. The center of the spherical surface lies 4m below the bottom of the cylinder. Please calculate the spherical surface's radius and the ca - Elevation
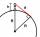 What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km. - Intersection 40981
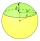 The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
- Spherical cap
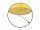 Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap. - Sphere parts, segment
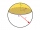 A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume of the segment and the surface of the segment?
A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume of the segment and the surface of the segment? - Stadium
 A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter.
A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter. - Spherical cap
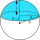 Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap).
Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap). - The hemisphere
 The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees?
The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees?
- Above Earth
 To what height must a boy be raised above the earth to see one-fifth of its surface?
To what height must a boy be raised above the earth to see one-fifth of its surface? - Sphere - parts
 Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 10 cm and a height v = 3.4 cm.
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 10 cm and a height v = 3.4 cm. - Spherical cap
 The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut.
The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut. - Spherical cap
 From the sphere with a radius of 11 was a truncated spherical cap. Its height is 6. What part of the volume is a spherical cap from the whole sphere?
From the sphere with a radius of 11 was a truncated spherical cap. Its height is 6. What part of the volume is a spherical cap from the whole sphere? - Calculate 65354
 Calculate the surface of a spherical paragraph with a height of 6 cm and a radius of 15 cm
Calculate the surface of a spherical paragraph with a height of 6 cm and a radius of 15 cm
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
