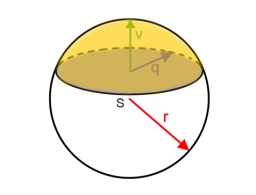
Spherical cap

Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm2. Determine the radius r of the sphere from which the spherical cap was cut.

Correct answer:

r =  3.0683 cm

Step-by-step explanation:


Try another example


Did you find an error or inaccuracy? Feel free to write us. Thank you!



avatar




Tips to related online calculators
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:


 
We encourage you to watch this tutorial video on this math problem: video1   video2   video3

Related math problems and questions:

  • Spherical cap
    Spherical_cap The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut.
  • Spherical cap 4
    spherical cap What is the surface area of a spherical cap, the base diameter 20 m, height 2.5 m? Calculate using formula.
  • Sphere - parts
    odsek_vusek Calculate the area of a spherical cap, which is part of an area with base radius ρ = 9 cm and a height v = 3.1 cm.
  • A spherical segment
    Spherical_sector A spherical section whose axial section has an angle of j = 120° in the center of the sphere is part of a sphere with a radius r = 10 cm. Calculate the cut surface.
  • Spherical section cut
    gulovy_odsek Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
  • Spherical cap
    kulova_usec From the sphere of radius 11 was truncated spherical cap. Its height is 6. What part of the volume is a spherical cap from the whole sphere?
  • Sphere parts, segment
    gulovy_odsek A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. .What are the volume of the segment and the surface of the segment?
  • Spherical cap
    koule2 What is the surface area of a spherical cap, the base diameter 20 m, height 2 m.
  • Hemisphere cut
    odsek_gule Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm.
  • Axial cut of a rectangle
    cylinder_cut Calculate the volume and surface of the cylinder whose axial cut is a rectangle 15 cm wide with a diagonal of 25 cm long.
  • Surface of the cylinder
    valec Calculate the surface of the cylinder for which the shell area is Spl = 20 cm2 and the height v = 3.5 cm
  • Spherical segment
    circular_segment The spherical segment with height h=1 has a volume V=223. Calculate the radius of the sphere of which is cut this segment.
  • Airplane
    tu-144 Aviator sees part of the earth's surface with an area of 200,000 square kilometers. How high he flies?
  • Frustrum - volume, area
    frustum-of-a-right-circular-cone Calculate the surface and volume of the truncated cone, the radius of the smaller figure is 4 cm, the height of the cone is 4 cm and the side of the truncated cone is 5 cm.
  • Sphere cut
    odsek_gule A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
  • Triangular prism
    prism3 The triangular prism has a base in the shape of a right triangle, the legs of which is 9 cm and 40 cm long. The height of the prism is 20 cm. What is its volume cm3? And the surface cm2?
  • Cap
    cone_hat Jesters hat is shaped by a rotating cone. Calculate how much paper is needed to the cap 54 cm high when the head circumference is 47 cm.