Two Sections
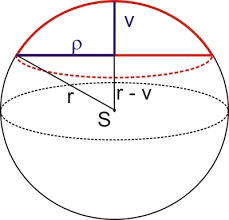
A sphere with a radius of 5 cm was divided into two spherical sections. The height of the smaller section is 1cm. Determine the volume of the smaller section to the nearest hundredth of a cm3.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
solid geometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cross-sections of a cone
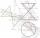Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Stadium
A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter. - The radius 4
The radius of a sphere is r=9 cm. What is the volume of this sphere? Use π ≈ 3.14 and round your answer to the nearest hundredth. cubic millimeters - Hemisphere layer
Find the volume of the spherical layer that results from a hemisphere with a radius of 5 cm by cutting a paragraph whose height is 1.5 cm.
- Hemisphere cut
Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm. - Spherical cap
From the sphere with a radius of 26 was a truncated spherical cap. Its height is 2. What part of the volume is a spherical cap from the whole sphere? - Spherical cap
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
