Sphere - parts
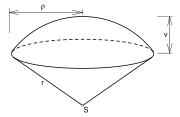
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our Density units converter will help you convert density units.
Do you want to round the number?
See also our trigonometric triangle calculator.
Tip: Our Density units converter will help you convert density units.
Do you want to round the number?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Spherical sector
Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm. - Spherical cap
The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut. - Spherical segment
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r = 5 cm and the radius of the circular base of the segment ρ = 4 cm. - Calculate sphere cap
Calculate the surface of a spherical cap with a height of 6 cm and a radius of 15 cm - Spherical cap
Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap). - Spherical cap 4
What is the surface area of a spherical cap, the base diameter of 20 m, and the height of 2.5 m? Calculate using the formula. - Spherical cap
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
