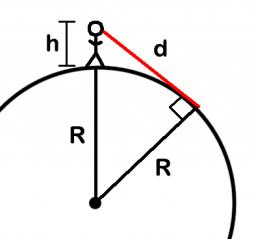
Elevation
What must be an observer's elevation so that he may see an object on the Earth 536 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsGrade of the word problem
Related math problems and questions:
- Horizon
The top of a lighthouse is 19 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.] - Earth rotation
How fast is the place on the Earth's equator moving if the Earth's radius is 6378 km? - Observer's 82805
An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly? - The spacecraft
The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considere
- Rotation of the Earth
Calculate the circumferential speed of the Earth's surface at a latitude of 34.5°. Consider a globe with a radius of 6378 km. - Above Earth
To what height must a boy be raised above the earth to see one-fifth of its surface? - Hot air balloon
The center of the balloon is at an altitude of 600 m above the ground (AGL). The observer on earth sees the center of the balloon at an elevation angle of 38°20'. The balloon is seen from the perspective of an angle of 1°16'. Calculate the diameter of the
