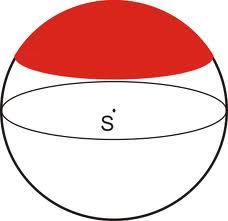
Spherical cap
From a sphere with radius 26, a spherical cap was cut. Its height is 2. What part of the volume is a spherical cap from the whole sphere?
Final Answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetricsbasic operations and conceptsnumbersUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Spherical cap
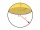 Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap. - Spherical sector
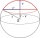 Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm.
Calculate the volume and surface area of a spherical sector if the spherical segment that is part of the sector has a base radius r1 = 6 cm and a height v = 2 cm. - Two Sections
 A sphere with a radius of 5 cm was divided into two spherical sections. The height of the smaller section is 1cm. Determine the volume of the smaller section to the nearest hundredth of a cm³.
A sphere with a radius of 5 cm was divided into two spherical sections. The height of the smaller section is 1cm. Determine the volume of the smaller section to the nearest hundredth of a cm³. - Sphere cut
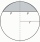 A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere?
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Hemisphere cut
 Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm.
Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm. - Spherical tank
 The water tower tank is a sphere with a radius of 35ft. If the tank is filled to one-quarter full, what is the height of the water?
The water tower tank is a sphere with a radius of 35ft. If the tank is filled to one-quarter full, what is the height of the water? - Sphere - parts
 Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm.
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm.
