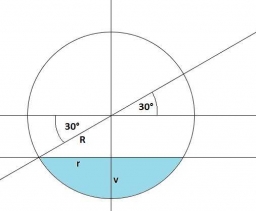
The hemisphere
The hemisphere container is filled with water. What is the radius of the container when 10 liters of water pour from it when tilted 30 degrees?
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you know the volume and unit volume, and want to convert volume units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you know the volume and unit volume, and want to convert volume units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- solid geometry
- sphere
- spherical cap
- hemisphere
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- goniometry and trigonometry
- sine
- cosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Water container
The cube-shaped container is filled to two-thirds of its height. If we pour 18 liters, it will be filled to three-fifths of the height. What is the volume of the whole container? - Water overflow
A rectangular container has a length of 30 cm, a width of 20 cm, and a height of 24 cm. It is filled with water to a depth of 15 cm. Some water overflows when an additional 6.5 liters of water is poured into the container. How many liters of water overflo - Temperature 36991
Honza filled 2 liters of hot water at a temperature of 90 °C from a heater into a five-liter container. What temperature must the water that the container fills have a mixture temperature of 42 °C? - Cylindrical 6636
A cylindrical container with a bottom diameter of 30 cm and a height of 20 cm is filled with water. We want to pour the water into another cylindrical container with a bottom diameter of 15 cm. What minimum height must the second container have for the wa
- Cylindrical 24211
The cylindrical container is completely filled and contains 62.8 liters of water. It is half a meter high. Calculate the bottom diameter. - Hemispherical hollow
The vessel's hemispherical hollow is filled with water to a height of 10 cm =. How many liters of water are inside if the hollow's inside diameter is d = 28cm? - Prism-shaped 6137
The prism-shaped vessel with a rhomboid base has one base diagonal of 10 cm and the edge of the base 14 cm. The edge of the base and the prism height are in a ratio of 2:5. How many liters of water is in the container when it is filled to four-fifths of t
