Polokoule 2
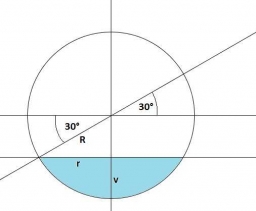
Nádoba tvaru polokoule je zcela naplněna vodou. Jaký poloměr má nádoba, když z ní při naklonění o 30 stupňů vyteče 10 l vody?
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Hmotnost vody v nádobě
Půlkruhová nádoba na ryby je naplněna vodou a má průměr 10 stop. Jaká je celková hmotnost vody zaokrouhlená na nejbližší libru v nádrži, pokud voda váží 62,5 libry na kubickou stopu? - Polokoule
Nádoba tvaru duté polokoule je naplněna vodou do výšky v = 10 cm. Kolik litrů vody obsahuje, pokud vnitřní průměr nádoby je d = 28cm? - Válec + čtyřstěn
Nádoba tvaru rotačního válce o poloměru podstavy 5 cm je naplněna vodou. O co stoupne hladina vody v nádobě, ponoříme-li do ní pravidelný čtyřstěn o hraně 7 cm. - Nádoba
Nádoba tvaru kostky je naplněna vodou do poloviny své výšky. Pokud dolijeme 20 l vody, bude nádoba naplněna do tří čtvrtin své výšky. Jaký je objem celé nádoby? - Kužel s průměrem
Nádoba tvaru kužele s průměrem dna 60 cm a boční stranou délky 0,5 m je zcela naplněna vodou. Vodu přelijeme do nádoby, která má tvář válce o poloměru 3 dm a výšce 20 cm. Bude válec přetékat, nebo naopak nebude plný? Vypočítejte kolik vody přeteče, nebo n - Nádoba 16
Nádoba tvaru válce obsahuje 62,8 litrů vody a je zcela naplněna. Výška nádoby je půl metru. Vypočítejte průměr dna. - Nádoba
Nádoba tvaru kvádru má výšku 52 cm a čtvercovou podstavu. Nádoba byla naplněna až po okraj vodou, pak jsme do ní ponořili kovovou kostku, což způsobilo, že z nádoby vyteklo 2,7 l vody. Po vytažení kostky z vody poklesla hladina vody v nádobě o 12 cm. Koli
