Pologuľa
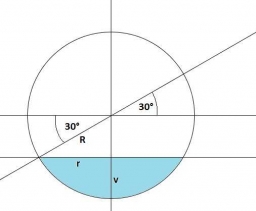
Nádoba tvaru pologule je úplne naplnená vodou. Aký polomer má nádoba, keď z nej pri naklonení o 30 stupňov vytečie 10 l vody?
Vaša odpoveď:
Vaša odpoveď:
Zobrazujem 3 komentáre:
Žiak
30 není hodnota velikosti úhlu, ale výsledek výpočtu. Dle vašeho značení:
sin 30 = (R – v)/R = 1/2 => v = R/2, cos 30 = r/R = sqrt(3)/2 => r = R*sqrt(3)/2
a dosadíte do V2.
V= V1 + V2 = 2/3*pi*R3 = 10 + V2 => R = 2* (30/11/pi)^(1/3) dm = cca 19,079 cm
:-)
sin 30 = (R – v)/R = 1/2 => v = R/2, cos 30 = r/R = sqrt(3)/2 => r = R*sqrt(3)/2
a dosadíte do V2.
V= V1 + V2 = 2/3*pi*R3 = 10 + V2 => R = 2* (30/11/pi)^(1/3) dm = cca 19,079 cm
:-)
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebrastereometriaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Nádoba - štvorsten
Nádoba tvaru rotačného valca s polomerom podstavy 5 cm je naplnená vodou. O čo stúpne hladina vody v nádobe, ak do nej ponoríme pravidelný štvorsten s hranou 7 cm. - Nádoba 14
Nádoba tvaru kocky je naplnená vodou do polovice svojej výšky. Ak dolejeme 20 l vody, bude nádoba naplnená do troch štvrtín svojej výšky. Aký je objem celej nádoby? - Nádoba kužeľ
Nádoba tvaru kužeľa s priemerom dna 60 cm a bočnou stranou dĺžky 0,5 m je úplne naplnená vodou. Vodu prelejeme do nádoby, ktorá má tvár valca o polomere 3 dm a výške 20 cm. Bude valec pretekať, alebo naopak nebude plný? Vypočítajte koľko vody pretečie, al - Priemer nádoby
Nádoba tvaru valca obsahuje 62,8 litra vody a je úplne naplnená. Výška nádoby je pol metra. Vypočítajte priemer dna. - Pretečie
Obdĺžniková nádoba, ktorá má dĺžku 30 cm, šírku 20 cm a výšku 24 cm, je naplnená vodou do hĺbky 15 cm. Keď sa do nádoby naleje ďalších 6,5 litra vody, časť vody pretečie. Koľko litrov vody pretečie nádobu? - Nádoba 11
Nádoba tvaru dutej polgule je naplnená vodou do výšky v=10 cm. Koľko litrov vody obsahuje, ak vnútorný priemer nádoby je d= 28cm? - Nádoba 16
Nádoba tvaru kvádra má výšku 52 cm a štvorcovú podstavu. Nádoba bola naplnená až po okraj vodou, potom sme do nej ponorili kovovú kocku, čo spôsobilo, že z nádoby vytieklo 2,7 l vody. Po vytiahnutí kocky z vody poklesla hladina vody v nádobe o 12 cm. Koľk
