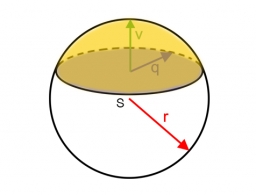
Spherical section cut
Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
Your answer:
Your answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
See also our right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circle arc + section
Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees. - Central angle calculation
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Circular grass seed
How many kg of grass seed must be bought to start a lawn in the shape of a circular section with a radius of r= 15 m and a central angle of 45 degrees if 1 g of grass seed is used per 1 dm of the square area? - Spherical sector
The spherical sector has axial section has an angle of α = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the surface of this spherical sector. - Circular segment
What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²? - Central angle 2 What is the arc length of a circle with a radius of 12 cm and a central angle of 255 degrees? A. 8.5 cm B. 12π cm C. 24π cm D. 17π cm
- Circular section area
Calculate the area of a circular section given by an angle of 220 degrees if the circle's radius is 20 cm. Round the result to cm2
