Tropics and polar zones
What percentage of the Earth's surface lies in the tropical, temperate, and polar zones?
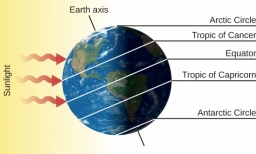
Tropics border individual zones at 23°27' and polar circles at 66°33'.
Your answer:
Tropics border individual zones at 23°27' and polar circles at 66°33'.
Your answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Tropical, mild and arctic
How many percent of the Earth's surface lies in the tropical, mild, and arctic ranges? The border between the ranges is the parallel 23°27' and 66°33'. - Rotation of the Earth
Calculate the linear speed of the Earth's surface at a latitude of 34.5°. Assume a globe with a radius of 6378 km. - Earth parallel
The Earth's radius is 6377 km. Calculate the circumference of the parallel at latitude 75°. - Meridian
What is the arc length of the Earth's meridian corresponding to 41° if the radius of the Earth is 6370 km? - Big Earth
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km. - The space
The space rocket orbits the Earth at an altitude of 400 km above the Earth's surface. Determine the magnitude of the centrifugal acceleration of the missile in its orbit. - The spacecraft
The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615 km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is consider
